Elliptic Curves Cryptographie (ECC)

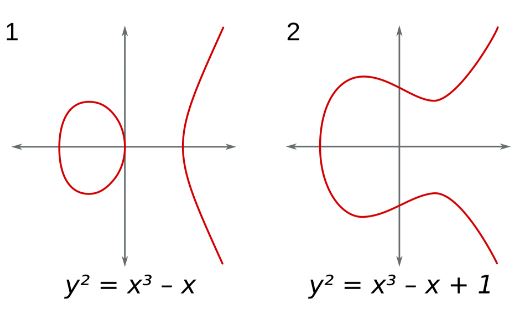
Elliptische Funktionen sind Funktionen der Form: y² = x³ + a * x + b. Dabei sind a und b reelle Parameter und (um Singularitäten auszuschließen) 4*a³+27*b² ≠ 0.

Die Graphen der Funktionen haben eine Form wie im Bild angegeben. Dabei kann die Ausbuchtung in der Größe variieren oder sich sogar separieren. Man sieht, elliptische Kurven sind zur x-Achse achsensymmetrisch.

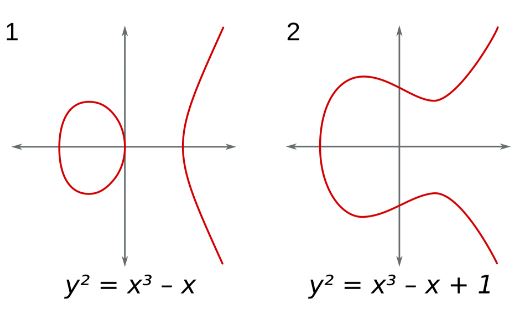
Man kann nun eine 'Addition' von Punkten auf elliptischen Kurven definieren und mit ihnen 'rechnen'.

Sei R die Summe der Punkte P(x_P/y_P) und Q(x_Q/y_Q), also R = P + Q.

Geometrisch ist diese Addition so zu verstehen: Man bildet die Sekante der auf einer gegebenen elliptischen Kurve gelegenen Punkte P und Q. Der (dritte) Schnittpunkt dieser Sekante mit der elliptischen Kurve R' wird an der x-Achse gespiegelt und man erhält den Punkt R. Rechnerisch lässt sich R einfach ermitteln: Man setzt die Sekante gleich der ell. Kurve und erhält eine Gleichung dritten Grades. Da bereits zwei Nullstellen bekannt sind (P und Q), kann man die dritte Nullstelle leicht bestimmen. Falls P = Q gilt, wird die Sekante durch die Tangente ersetzt.

Man errechnet :

x_R = m² - x_P - x_Q und

y_R = -y_P + m * ( x_P - x_R)

Sekantensteigung m = (y_Q - y_P) / (x_Q - x_P) mit P ≠ Q

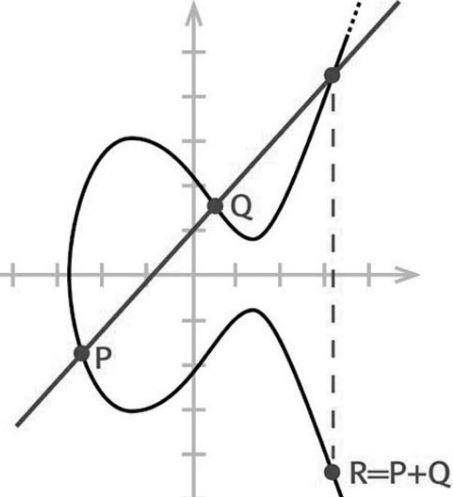
Tangentensteigung m = (3 * x_P² + a) / (2 * y_P) mit y_P ≠ 0 und P = Q.

Nun kann man auch Punkte verdoppeln: R = 2 * P = P + P.

Die Falltüreigenschaft für das Verschlüsseln erhält man , weil es relativ leicht ist, aus einem gegebenen Startwert P einer gegebenen elliptischen Funktion R = n * P zu berechnen mit n ∊N, aber es ist sehr schwierig, aus R auf n zu schließen.

Um Rundungsfehler bei diesen Berechnungen auszuschließen, führt man die Rechnungen nicht über den reellen Zahlen aus, sondern man verwendet einen Primkörper, rechnet also immer modulo p mit p ist Primzahl. Dieser Körper hat dann p verschiedene Elemente. Die Schlüssellänge gibt die maximale Größe von p vor - bei einer Schlüssellänge von 512 bit entspricht das etwa (mit 2¹⁰ ∼ 1000) einer 170stelligen Dezimalzahl. Die kürzere sichere Schlüssellänge gegenüber anderen Verfahren (z.B. RSA) ist für den Einsatz von Smartcards wegen deren begrenztem Speicher von Bedeutung.

Für die Verschlüsselung betrachtet man folglich die Lösungen der Weierstrass-Gleichung:
(y² - x³ - a * x - b) mod p = 0, a,b∊{0,...,p-1} und p Primzahl.

Für die Lösungen x und y gilt ebenfalls: x,y∊{0,...,p-1}

Die Anzahl der Punkte k (also die Anzahl der Lösungen der Gleichung) lässt sich mit dem Satz von Hasse abschätzen:
p + 1 - 2* √p ≤ k ≤ p + 1 + 2 * √p

Beispielrechnungen:

Bei der Verschlüsselung mittels Elliptischer Kurven legen die beiden Parteien eine elliptische Funktion (also die Parameter a und b sowie die Primzahl p und auch den erzeugenden Punkt P öffentlich fest. Jede Partei wählt jetzt eine geheime (private) Zahl A bzw B kleiner als p. Dann überträgt jede Partei öffentlich A*P bzw B*P an die jeweils andere Partei. Mit dem geheimen Schlüssel kann jede Partei nun A*B*P bzw B*A*P berechnen. Das Ergebnis ist gleich und bildet nun den gemeinsamen geheimen Schlüssel mit dessen Hilfe die eigentlichen Daten verschlüsselt werden.

Es beruht darauf, dass es einfach ist, A*P zu berechnen, aber sehr schwer, aus P und A*P (beide öffentlich) auf A zu schließen.

Es können elliptische Kurven aus einem Brainpool verwendet werden (BSI- Bundesamt für Sicherheit in der Informationstechnik oder NIST - National Institute of Standards and Technology). Es ist dann z.B. sichergestellt, dass Startwerte nicht zu kleine Untergruppen erzeugen. Neuerdings werden auch allgemeinere elliptische Kurven empfohlen, z.B. die Curve25519, die auf der Gleichung y² = x³ + 486662 * x² + x in einem endlichen Körper modulo der Primzahl 2²⁵⁵ - 19 beruht (daher der Name).