f1(x) = 1 – x2 f2(x) = 2 ⋅ x3 + 3 ⋅ x2 – 12 ⋅ x + 1
b) Geben Sie die Quotientenregel an.
c) Wie lautet die Definition der 1.Ableitung?
d) An welcher Stelle hat der Graph der Funktion f(x) = x2 + x die Steigung m = 3? Geben Sie an der Stelle x = 4 die Steigung des Graphen an.
zu a)
Waagerechte Tangete → Steigung der Tangente ist Null.
Die Steigung der Tangente erhält man über die 1. Ableitung der Funktion, also → f '(x) = 0
f1'(x) = - 2 ⋅ x = 0 → x = 0
Der Graph der Funktion f1 hat an der Stelle x = 0 eine waagerechte Tangete.
f2'(x) = 6 ⋅ x2 + 6 ⋅ x - 12 = 0 → x1 = -2 und x2 = 1
Der Graph der Funktion f2 hat an den Stellen x1 = -2 und x2 = 1 eine waagerechte Tangete.
zu b)
Seien f und g differenzierbare Funktionen. Dann gilt: h(x) = → h '(x) =
zu c)
Die erste Ableitung einer Funktion f beschreibt die Änderungsrate dieser Funktion bezüglich ihrer Variablen. Sie gibt die Steigung der Tangente an den Graphen der Funktion an der Stelle x an.
$$f'(x)~=~\lim_{h \to 0} \frac {f(x+h) - f(x)} {h}$$
zu d)
Ansatz: f '(x) = 3 → 2 ⋅ x + 1 = 3 → x = 1
An der Stelle x = 1 hat der Graph der Funktion f(x) = x2 + x die Steigung m = 3.
Ansatz: f '(4) berechnen → 2 ⋅ 4 + 1 = 9
An der Stelle x = 4 hat der Graph von f die Steigung 9.
Waagerechte Tangete → Steigung der Tangente ist Null.
Die Steigung der Tangente erhält man über die 1. Ableitung der Funktion, also → f '(x) = 0
f1'(x) = - 2 ⋅ x = 0 → x = 0
Der Graph der Funktion f1 hat an der Stelle x = 0 eine waagerechte Tangete.
f2'(x) = 6 ⋅ x2 + 6 ⋅ x - 12 = 0 → x1 = -2 und x2 = 1
Der Graph der Funktion f2 hat an den Stellen x1 = -2 und x2 = 1 eine waagerechte Tangete.
zu b)
Seien f und g differenzierbare Funktionen. Dann gilt: h(x) = → h '(x) =
zu c)
Die erste Ableitung einer Funktion f beschreibt die Änderungsrate dieser Funktion bezüglich ihrer Variablen. Sie gibt die Steigung der Tangente an den Graphen der Funktion an der Stelle x an.
$$f'(x)~=~\lim_{h \to 0} \frac {f(x+h) - f(x)} {h}$$
zu d)
Ansatz: f '(x) = 3 → 2 ⋅ x + 1 = 3 → x = 1
An der Stelle x = 1 hat der Graph der Funktion f(x) = x2 + x die Steigung m = 3.
Ansatz: f '(4) berechnen → 2 ⋅ 4 + 1 = 9
An der Stelle x = 4 hat der Graph von f die Steigung 9.
| a) f(x) = 3x4 + 2x2 - 5x | b) f(x) = | c) f(u) = 5ax2 - 2u3x |
| d) f(a) = 5ax2 - 2a | e) f(x) = (2x - 2)-1 | f) f(x) = x ⋅ (4x + 1) -1 |
| g) f(x) = x ⋅ | h) f(x) = | i) f(x) = + |
| j) f(x) = 7x4 + 3x2 - | k) f(x) = (x + 3)4 ⋅ (2x - 6) | l) f(x) = 5ax2 - 2a |
a) f '(x) = 12x3 + 4x - 5
b) f '(x) =
c) f '(u) = -6u2x
d) f '(a) = 5x2 - 2
e) f '(x) = -2 ⋅ (2x - 2)-2
f) f '(x) = (4x + 1) -1 - 4x ⋅ (4x + 1) -2
g) f '(x) = + ⋅x ⋅ (7x3 + 2x)-0,5 ⋅ (21x2 + 2)
h) f '(x) =
i) f '(x) = ⋅ + ⋅
j) f '(x) = 28x3 + 6x +
k) f '(x) = 4⋅(x + 3)3 ⋅ (2x - 6) + 2⋅(x + 3)4
l) f '(x) = 10ax
b) f '(x) =
c) f '(u) = -6u2x
d) f '(a) = 5x2 - 2
e) f '(x) = -2 ⋅ (2x - 2)-2
f) f '(x) = (4x + 1) -1 - 4x ⋅ (4x + 1) -2
g) f '(x) = + ⋅x ⋅ (7x3 + 2x)-0,5 ⋅ (21x2 + 2)
h) f '(x) =
i) f '(x) = ⋅ + ⋅
j) f '(x) = 28x3 + 6x +
k) f '(x) = 4⋅(x + 3)3 ⋅ (2x - 6) + 2⋅(x + 3)4
l) f '(x) = 10ax
a) f(x) = 3x3+ 4x2 − 5 P = (3/?)
b) f(x) = x4 − 6x3 P = (−2/?)
zu a):
Ansatz: f '(3) berechnen mit f '(x) = 9 ⋅ x2 + 8 ⋅ x → f '(3) = 9 ⋅ 32 + 8 ⋅ 3 = 105
y-Koordinate des Punktes P berechnen: f(3) = 3 ⋅ 33 + 4 ⋅ 32 − 5 = 112 → P(3/112)
Im Punkt P(3/112) hat der Graph von f die Steigung 105.
zu b)
Ansatz: f '(-2) berechnen mit f '(x) = 4 ⋅ x3 - 18 ⋅ x2 → f '(-2) = 4 ⋅ (-2)3 - 18 ⋅ (-2)2 = -104
y-Koordinate des Punktes P berechnen: f(-2) = (-2)4 − 6 ⋅ (-2)3 = 64 → P(-2/64)
Im Punkt P(-2/64) hat der Graph von f die Steigung -104.
Ansatz: f '(3) berechnen mit f '(x) = 9 ⋅ x2 + 8 ⋅ x → f '(3) = 9 ⋅ 32 + 8 ⋅ 3 = 105
y-Koordinate des Punktes P berechnen: f(3) = 3 ⋅ 33 + 4 ⋅ 32 − 5 = 112 → P(3/112)
Im Punkt P(3/112) hat der Graph von f die Steigung 105.
zu b)
Ansatz: f '(-2) berechnen mit f '(x) = 4 ⋅ x3 - 18 ⋅ x2 → f '(-2) = 4 ⋅ (-2)3 - 18 ⋅ (-2)2 = -104
y-Koordinate des Punktes P berechnen: f(-2) = (-2)4 − 6 ⋅ (-2)3 = 64 → P(-2/64)
Im Punkt P(-2/64) hat der Graph von f die Steigung -104.
Ansatz: Die Aleitungsfunktionen gleichsetzen → f '(x) = g '(x)
f '(x) = -6x + 12 g '(x) = 6x2
Gleichetzen: -6x + 12 = 6x2 → 6x2 + 6x - 12 = 0 → x2 + x - 2 = 0 → x1 = -2 und x2 = 1
An der Stelle x1 = -2 haben die Funktionen die gleiche Steigung f '(-2) = g '(-2) = 24.
An der Stelle x2 = 1 haben die Funktionen die gleiche Steigung f '(1) = g '(1) = 6.
f '(x) = -6x + 12 g '(x) = 6x2
Gleichetzen: -6x + 12 = 6x2 → 6x2 + 6x - 12 = 0 → x2 + x - 2 = 0 → x1 = -2 und x2 = 1
An der Stelle x1 = -2 haben die Funktionen die gleiche Steigung f '(-2) = g '(-2) = 24.
An der Stelle x2 = 1 haben die Funktionen die gleiche Steigung f '(1) = g '(1) = 6.
a) Bestimmen Sie die Steigung der Kurve in den Schnittpunkten mit den Koordinatenachsen!
b) An welcher Stelle hat der Graph die Steigung 6?
c) An welcher Stelle hat der Graph eine waagerechte Tangente?
zu a)
Schnittpunkt mit der x-Achse berechnen: f(x) = 0 → x2 − 4x = 0 → x1 = 0 und x2 = 4 → P1(0/0) und P2(4/0)
Schnittpunkt mit der y-Achse berechnen: x = 0 → f(0) = 02 − 4 ⋅ 0 = 0 → P3(0/0) entspricht P1
jeweilige Steigungen bestimmen mit f '(x) = 2x - 4:
für P1: f '(0) = 2 ⋅ 0 - 4 = -4 → Die Steigung an den Graphen von f in P1 beträgt -4.
für P3: f '(4) = 2 ⋅ 4 - 4 = 4 → Die Steigung an den Graphen von f in P2 beträgt 4.
zu b)
Ansatz: f '(x) = 6 → 2x - 4 = 6 → x = 5
An der Stelle x = 5 hat der Graph die Steigung 6.
zu c)
Ansatz: f '(x) = 0 → 2x - 4 = 0 → x = 2
An der Stelle x = 2 hat der Graph eine waagerechte Tangente.
Schnittpunkt mit der x-Achse berechnen: f(x) = 0 → x2 − 4x = 0 → x1 = 0 und x2 = 4 → P1(0/0) und P2(4/0)
Schnittpunkt mit der y-Achse berechnen: x = 0 → f(0) = 02 − 4 ⋅ 0 = 0 → P3(0/0) entspricht P1
jeweilige Steigungen bestimmen mit f '(x) = 2x - 4:
für P1: f '(0) = 2 ⋅ 0 - 4 = -4 → Die Steigung an den Graphen von f in P1 beträgt -4.
für P3: f '(4) = 2 ⋅ 4 - 4 = 4 → Die Steigung an den Graphen von f in P2 beträgt 4.
zu b)
Ansatz: f '(x) = 6 → 2x - 4 = 6 → x = 5
An der Stelle x = 5 hat der Graph die Steigung 6.
zu c)
Ansatz: f '(x) = 0 → 2x - 4 = 0 → x = 2
An der Stelle x = 2 hat der Graph eine waagerechte Tangente.
a) Berechnen Sie die Kosten, wenn 3 bzw. 7 Einheiten produziert werden.
b) Jede Einheit wird zum Preis von 0,8 Geldeinheiten verkauft. Geben Sie die Gewinnfunktion an. Berechnen Sie den maximalen Gewinn.
zu a)
K(3) = ⋅33 - ⋅32 + 3 + 1 ≈ 2,73
K(7) = ⋅73 - ⋅72 + 7 + 1 ≈ 4,17
Wenn 3 Einheiten produziert werden, betragen die Kosten etwa 27300 €.
Wenn 7 Einheiten produziert werden, betragen die Kosten etwa 41700 €.
zu b)
Die Umsatzfunktion ist U(x) = 0,8 ⋅ x.
Die Gewinnfunktion ist G(x) = U(x) - K(x) = 0,8 ⋅ x - (⋅x3 - ⋅x2 + x + 1) = -⋅x3 + ⋅x2 - 0,2x - 1.
Um den maximalen Gewinn zu berechnen, muss ein Extremwert der Gewinnfunktion berechnet werden.
Notwendige Bedingung: G '(x) = 0 → G '(x) = -⋅x2 + x - 0,2 = 0 → x2 - 8x + = 0
Daraus folgt, mögliche Extremstellen sind x1 ≈ 0,575 sowie x2 ≈ 7,425
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung der hinreichenden Bedingung
mit G ''(x) = -⋅x + :
G ''(0,575) ≈ 0,32 > 0 → An der Stelle x1 liegt ein Minimum vor.
G ''(7,425) ≈ -0,32 < 0 → An der Stelle x2 liegt ein Maximum vor.
Maximalen Gewinn berechnen: G(7,425) = -⋅7,4253 + ⋅7,4252 - 0,2⋅7,425 - 1 → G(7,425) ≈ 1,46
Der Gewinn wird maximal, wenn etwa 7425 Rechner verkauft werden. Der Gewinn beträgt dann etwa 14600 €.
K(3) = ⋅33 - ⋅32 + 3 + 1 ≈ 2,73
K(7) = ⋅73 - ⋅72 + 7 + 1 ≈ 4,17
Wenn 3 Einheiten produziert werden, betragen die Kosten etwa 27300 €.
Wenn 7 Einheiten produziert werden, betragen die Kosten etwa 41700 €.
zu b)
Die Umsatzfunktion ist U(x) = 0,8 ⋅ x.
Die Gewinnfunktion ist G(x) = U(x) - K(x) = 0,8 ⋅ x - (⋅x3 - ⋅x2 + x + 1) = -⋅x3 + ⋅x2 - 0,2x - 1.
Um den maximalen Gewinn zu berechnen, muss ein Extremwert der Gewinnfunktion berechnet werden.
Notwendige Bedingung: G '(x) = 0 → G '(x) = -⋅x2 + x - 0,2 = 0 → x2 - 8x + = 0
Daraus folgt, mögliche Extremstellen sind x1 ≈ 0,575 sowie x2 ≈ 7,425
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung der hinreichenden Bedingung
mit G ''(x) = -⋅x + :
G ''(0,575) ≈ 0,32 > 0 → An der Stelle x1 liegt ein Minimum vor.
G ''(7,425) ≈ -0,32 < 0 → An der Stelle x2 liegt ein Maximum vor.
Maximalen Gewinn berechnen: G(7,425) = -⋅7,4253 + ⋅7,4252 - 0,2⋅7,425 - 1 → G(7,425) ≈ 1,46
Der Gewinn wird maximal, wenn etwa 7425 Rechner verkauft werden. Der Gewinn beträgt dann etwa 14600 €.
Es gilt:
$$f'(x)~=~\lim_{h \to 0} \frac {f(x+h) - f(x)} {h}~=~ \lim_{h \to 0}\frac{\frac{1}{x+h}-\frac{1}{x}}{h}~=~ \lim_{h \to 0}\frac{\frac{x-(x+h)}{(x+h)\cdot x}}{h}~=~ \lim_{h \to 0}\frac{\frac{-h}{(x+h)\cdot x}}{h}~=~ \lim_{h \to 0}\frac{-1}{(x+h)\cdot x}~=~ -\frac{1}{x^2}$$
$$f'(x)~=~\lim_{h \to 0} \frac {f(x+h) - f(x)} {h}~=~ \lim_{h \to 0}\frac{\frac{1}{x+h}-\frac{1}{x}}{h}~=~ \lim_{h \to 0}\frac{\frac{x-(x+h)}{(x+h)\cdot x}}{h}~=~ \lim_{h \to 0}\frac{\frac{-h}{(x+h)\cdot x}}{h}~=~ \lim_{h \to 0}\frac{-1}{(x+h)\cdot x}~=~ -\frac{1}{x^2}$$
a) jeweils gegenüberliegende Seiten sind parallel
b) alle Seiten sind gleich lang und es gibt vier rechte Winkel
c) es gibt vier rechte Winkel.
Kleine Anleihe aus der Logik: A und B seien Aussagen , die entweder wahr oder falsch sein können.
Gegeben sei eine Folgerung (oder Implikation): A → B (in Worten: 'Wenn A so B' oder auch 'aus A folgt B')
Anmerkung: A heißt Prämisse oder Voraussetzung und B Konklusion oder Behauptung.
Zur Begriffsbildung:
Die (wahre) Aussage A ist hinreichend, um die (wahre) Aussage B folgern zu können.
Die (wahre) Aussage B wiederum ist notwendig, falls die Aussage A wahr sein soll (, denn wenn A wahr ist, kann man daraus ja B folgern).
zu a)
Die Bedingung 'jeweils gegenüberliegende Seiten sind parallel' ist notwendig dafür, dass ein Trapez ein Rechteck ist, aber sie ist nicht hinreichend (denn es könnte dann auch eine Raute sein).
zu b)
Die Bedingung 'alle Seiten sind gleich lang und es gibt vier rechte Winkel' ist hinreichend dafür, dass ein Trapez ein Rechteck ist, aber sie ist nicht notwendig (denn das Rechteck muss kein Quadrat sein).
zu c)
Die Bedingung 'es gibt vier rechte Winkel' ist hinreichend dafür, dass ein Trapez ein Rechteck ist, und sie ist auch notwendig.
Gegeben sei eine Folgerung (oder Implikation): A → B (in Worten: 'Wenn A so B' oder auch 'aus A folgt B')
Anmerkung: A heißt Prämisse oder Voraussetzung und B Konklusion oder Behauptung.
Zur Begriffsbildung:
Die (wahre) Aussage A ist hinreichend, um die (wahre) Aussage B folgern zu können.
Die (wahre) Aussage B wiederum ist notwendig, falls die Aussage A wahr sein soll (, denn wenn A wahr ist, kann man daraus ja B folgern).
zu a)
Die Bedingung 'jeweils gegenüberliegende Seiten sind parallel' ist notwendig dafür, dass ein Trapez ein Rechteck ist, aber sie ist nicht hinreichend (denn es könnte dann auch eine Raute sein).
zu b)
Die Bedingung 'alle Seiten sind gleich lang und es gibt vier rechte Winkel' ist hinreichend dafür, dass ein Trapez ein Rechteck ist, aber sie ist nicht notwendig (denn das Rechteck muss kein Quadrat sein).
zu c)
Die Bedingung 'es gibt vier rechte Winkel' ist hinreichend dafür, dass ein Trapez ein Rechteck ist, und sie ist auch notwendig.
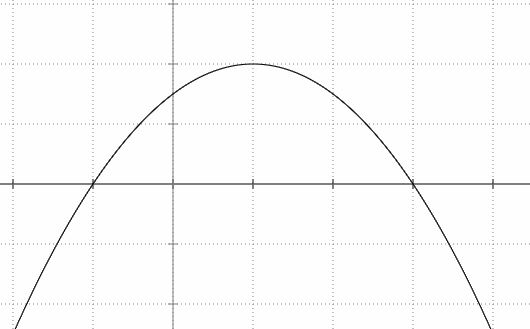 Das Bild zeigt den Graphen einer Ableitungsfunktion f ’. Skizzieren Sie die Graphen der Funktionen f ’’ sowie f.
Das Bild zeigt den Graphen einer Ableitungsfunktion f ’. Skizzieren Sie die Graphen der Funktionen f ’’ sowie f. 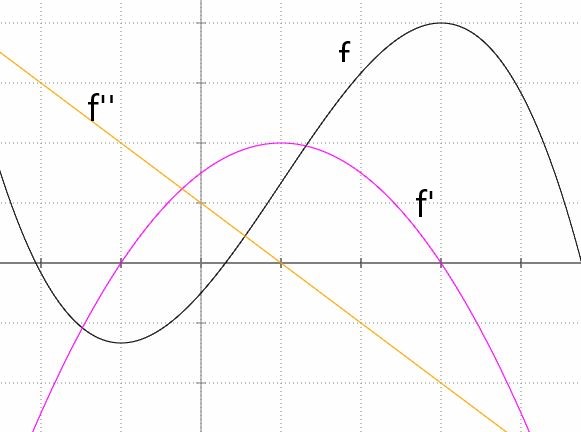 Der Graph von f ist nicht eindeutig. Er kann entlang der y-Achse verschoben werden.
Der Graph von f ist nicht eindeutig. Er kann entlang der y-Achse verschoben werden.Seine Kosten werden durch die Funktion K(x) = ⋅ x3 - 2⋅x2 + 10⋅x + 250 beschrieben. Dabei gibt x die Anzahl der Säcke an.
a) Zeigen Sie, dass sich die Gewinnfunktion durch G(x) = -⋅ x3 + 2⋅x2 + 50⋅x - 250 darstellen lässt.
b) Ermitteln Sie die Produktionsmenge, bei der der Gewinn am größten ist. Geben Sie diesen an.
c) Durch die Finanzkrise kann er nur noch 40 Säcke verkaufen. Macht er trotzdem noch Gewinn? Wie viele Säcke muss er mindestens verkaufen, um einen Gewinn zu erzielen (Probieren!)?
zu a)
Die Umsatzfunktion ist U(x) = 60 ⋅ x.
Die Gewinnfunktion ist G(x) = U(x) - K(x) = 60 ⋅ x - (⋅ x3 - 2⋅x2 + 10⋅x + 250) = -⋅ x3 + 2⋅x2 + 50⋅x - 250.
zu b)
Um den maximalen Gewinn zu berechnen, muss ein Extremwert der Gewinnfunktion berechnet werden.
Notwendige Bedingung: G '(x) = 0 → G '(x) = -0,1⋅x2 + 4⋅x + 50 = 0 → x2 - 40x - 500 = 0
Daraus folgt, mögliche Extremstellen sind x1 = -10 sowie x2 = 50.
Negative Werte liegen nicht im Definitionsbereich.
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung der hinreichenden Bedingung
für x2 mit G ''(x) = -0,2⋅x + 4:
G ''(50) = -6 < 0 → An der Stelle x2 liegt ein Maximum vor.
Gewinn berechnen: G(50) = 3083
Der Gewinn wird maximal, wenn 50 Säcke verkauft werden. Der Gewinn beträgt dann 3083,33 €.
zu c)
G(40) berechnen:
G(40) ≈ 2816,67 → Bei 40 verkauften Säcken beträgt der Gewinn 2816,67 €.
G(5) ≈ 45,83 → Bei 5 verkauften Säcken beträgt der Gewinn 45,83 €.
G(4) ≈ -20,13 → Bei 4 verkauften Säcken beträgt der Verlust 20,13 €.
Er muss mindestens 5 Säcke verkaufen, um einen Gewinn zu erzielen. (Anmerkung: Ab 78 Säcken macht er wieder Verlust.)
Die Umsatzfunktion ist U(x) = 60 ⋅ x.
Die Gewinnfunktion ist G(x) = U(x) - K(x) = 60 ⋅ x - (⋅ x3 - 2⋅x2 + 10⋅x + 250) = -⋅ x3 + 2⋅x2 + 50⋅x - 250.
zu b)
Um den maximalen Gewinn zu berechnen, muss ein Extremwert der Gewinnfunktion berechnet werden.
Notwendige Bedingung: G '(x) = 0 → G '(x) = -0,1⋅x2 + 4⋅x + 50 = 0 → x2 - 40x - 500 = 0
Daraus folgt, mögliche Extremstellen sind x1 = -10 sowie x2 = 50.
Negative Werte liegen nicht im Definitionsbereich.
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung der hinreichenden Bedingung
für x2 mit G ''(x) = -0,2⋅x + 4:
G ''(50) = -6 < 0 → An der Stelle x2 liegt ein Maximum vor.
Gewinn berechnen: G(50) = 3083
Der Gewinn wird maximal, wenn 50 Säcke verkauft werden. Der Gewinn beträgt dann 3083,33 €.
zu c)
G(40) berechnen:
G(40) ≈ 2816,67 → Bei 40 verkauften Säcken beträgt der Gewinn 2816,67 €.
G(5) ≈ 45,83 → Bei 5 verkauften Säcken beträgt der Gewinn 45,83 €.
G(4) ≈ -20,13 → Bei 4 verkauften Säcken beträgt der Verlust 20,13 €.
Er muss mindestens 5 Säcke verkaufen, um einen Gewinn zu erzielen. (Anmerkung: Ab 78 Säcken macht er wieder Verlust.)
a) Welche Geschwindigkeit hat er nach 0,5 Sekunden?
b) Wie groß ist seine Geschwindigkeit beim Eintauchen in das Wasser?
zu a)
Die Geschwindigkeit-Zeit-Funktion ist die erste Ableitung der Weg-Zeit-Funktion: v(t) = h'(t) = -9,6⋅t
Dann v(0,5) = -9,6⋅t = -4,8
Nach 0,5 s besitzt er eine Geschwindigkeit von -4,8 .
Das Minuszeichen drückt aus, dass die Geschwindigkeit nach unten gerichtet ist.
zu b)
Zuerst ist die Zeit bis zum Eintauchen zu berechnen. Es gilt: h(t) = 0 = 10 – 4,8t2 → t = s
Nun in die Geschwindigkeitsfunktion einsetzen: v() = -9,6⋅ = -20
Beim Eintauchen besitzt der Springer eine Geschwindigkeit von v = -20 = -72 .
Die Geschwindigkeit-Zeit-Funktion ist die erste Ableitung der Weg-Zeit-Funktion: v(t) = h'(t) = -9,6⋅t
Dann v(0,5) = -9,6⋅t = -4,8
Nach 0,5 s besitzt er eine Geschwindigkeit von -4,8 .
Das Minuszeichen drückt aus, dass die Geschwindigkeit nach unten gerichtet ist.
zu b)
Zuerst ist die Zeit bis zum Eintauchen zu berechnen. Es gilt: h(t) = 0 = 10 – 4,8t2 → t = s
Nun in die Geschwindigkeitsfunktion einsetzen: v() = -9,6⋅ = -20
Beim Eintauchen besitzt der Springer eine Geschwindigkeit von v = -20 = -72 .
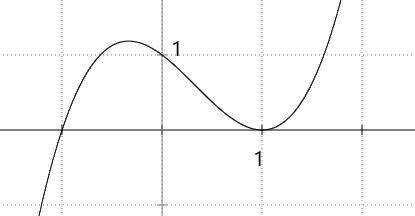
1. Ableitungen:
f '(x) = 3⋅x2 - 2⋅x - 1 f ''(x) = 6⋅x - 2 f '''(x) = 6
2. Symmetrie:
Die Funktion ist weder punkt- noch achsensymmetrisch, denn f ist eine ganzrationale Funktion mit geraden und ungeraden Exponenten.
3. Schnittpunkte mit den Achsen:
Schnittpunkt mit der x-Achse sind Nullstellen:
Ansatz: f(x) = 0
Erste Nullstelle raten mit x1 = 1 → dann Polynomdivision (x3 – x2 – x + 1) : (x-1) = x2 - 1
Aus x2 - 1 = 0 → x2 = 1 und x3 = -1
Insgesamt: Nullstellen sind N1 (1/0) sowie N2 (-1/0)
Da N1 doppelte Nullstelle ist, liegt an der Stelle x = 1 ein Berührpunkt der x-Achse vor.
Schnittpunkt mit der y-Achse: f(0) = 1 → (0/1) ist der Schnittpunkt des Graphen von f mit der y-Achse
4. Extremwerte.
Notwendige Bedingung: f '(x) = 0 → f '(x) = 3⋅x2 - 2⋅x - 1 = 0 → x2 - x - = 0
Daraus folgt, mögliche Extremstellen sind x1 = - sowie x2 = 1.
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung f ''(xi) = 6⋅xi - 2 ≠ 0:
f ''(-) = 6⋅(-) - 2 = -4 < 0 → E1(-/-) ist rel. Maximum
f ''(1) = 6⋅1 - 2 = 4 > 0 → E2(1/0) ist rel. Minimum.
5. Wendepunkte:
Notwendige Bedingung: f ''(x) = 0 → f ''(x) = 6⋅x - 2 = 0 → x = ist mögliche Wendestelle.
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung f '''() = 6 ≠ 0.
Daraus folgt: W(/) ist Wendepunkt vom Graphen von f.
6. Verhalten für sehr kleine und sehr große x:
$$\lim_{x \to -\infty} f(x)~=~-\infty ~~~~~~~~~\lim_{x \to +\infty} f(x)~=~+\infty$$
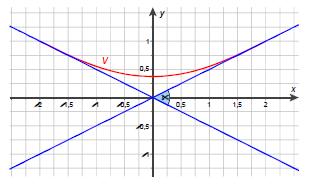 Kalli ist frischgebackener Straßenbauer und hat von seinem Chef einen ersten Großauftrag bekommen. Kalli soll die Kreuzung, die durch zwei geradlinig verlaufende Straßen gebildet wird,
durch den Neubau des Verbindungsstücks V entlasten. Die Verbindungskurve wird durch den Graphen einer Funktion f beschrieben. Die geradlinigen Straßen können durch die
Funktion g1(x) = 0,5⋅x und g2(x) = -0,5⋅x beschrieben werden (s.Skizze; 1 Einheit entspricht 1 km).
Kalli ist frischgebackener Straßenbauer und hat von seinem Chef einen ersten Großauftrag bekommen. Kalli soll die Kreuzung, die durch zwei geradlinig verlaufende Straßen gebildet wird,
durch den Neubau des Verbindungsstücks V entlasten. Die Verbindungskurve wird durch den Graphen einer Funktion f beschrieben. Die geradlinigen Straßen können durch die
Funktion g1(x) = 0,5⋅x und g2(x) = -0,5⋅x beschrieben werden (s.Skizze; 1 Einheit entspricht 1 km).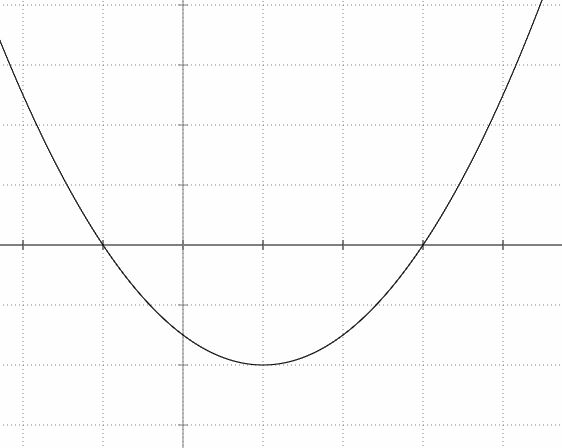 Das Bild zeigt den Graphen einer Ableitungsfunktion f ’. Skizzieren Sie die Graphen der Funktionen f ’’ sowie f.
Das Bild zeigt den Graphen einer Ableitungsfunktion f ’. Skizzieren Sie die Graphen der Funktionen f ’’ sowie f.
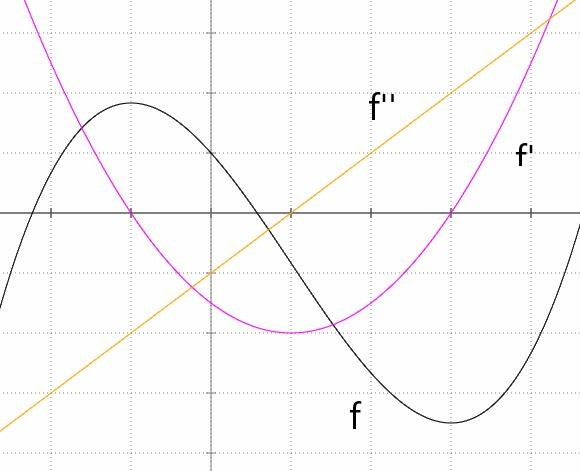 Der Graph von f ist nicht eindeutig. Er kann entlang der y-Achse verschoben werden.
Der Graph von f ist nicht eindeutig. Er kann entlang der y-Achse verschoben werden.