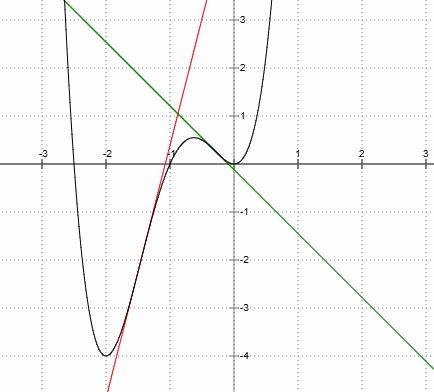
Führen Sie eine Kurvendiskussion durch und bestimmen Sie den Schnittpunkt der Wendetangenten.
 1. Ableitungen:
1. Ableitungen: f '(x) = 8⋅x3 + 21⋅x2 + 10⋅x f ''(x) = 24⋅x2 + 42⋅x + 10 f '''(x) = 48⋅x + 42
2. Symmetrie:
Die Funktion ist weder punkt- noch achsensymmetrisch, denn f ist eine ganzrationale Funktion mit geraden und ungeraden Exponenten.
3. Schnittpunkte mit den Achsen:
Schnittpunkt mit der x-Achse sind Nullstellen:
Ansatz: f(x) = 0
Ausklammern: x2 ⋅ (2⋅x2 + 7⋅x + 5) = 0 → x1 = 0 ist doppelte Nullstelle
Aus 2⋅x2 + 7⋅x + 5 = 0 → x2 = -2,5 und x3 = -1
Insgesamt: Nullstellen sind N1 (0/0) , N2 (-2,5/0) sowie N3 (-1/0)
Da N1 doppelte Nullstelle ist, liegt an der Stelle x = 0 ein Berührpunkt der x-Achse vor.
Schnittpunkt mit der y-Achse: f(0) = 0 → (0/0) ist der Schnittpunkt des Graphen von f mit der y-Achse
4. Extremwerte.
Notwendige Bedingung: f '(x) = 0 → f '(x) = 8⋅x3 + 21⋅x2 + 10⋅x = x ⋅ (8⋅x2 + 21⋅x + 10) = 0
→ xE1 = 0 oder (8⋅x2 + 21⋅x + 10) = 0
aus x2 + x + = 0 → xE2 = -2 oder xE3 = -0,625
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die
hinreichende Bedingung f ''(xi) = 24⋅x2 + 42⋅x + 10 ≠ 0:
f ''(0) = 24⋅02 + 42⋅0 + 10 = 10 > 0 → E1(0/0) ist rel. Minimum
f ''(-2) = 24⋅(-2)2 + 42⋅(-2) + 10 = 190 > 0 → E2(-2/-4) ist rel. Minimum.
f ''(-0,625) = 24⋅(-0,625)2 + 42⋅(-0,625) + 10 = -6,875 < 0 → E3(-0,625/0,549) ist rel. Maximum.
5. Wendepunkte:
Notwendige Bedingung: f ''(x) = 0 → f ''(x) = 24⋅x2 + 42⋅x + 10 = 0
→ x1 ≈ -1,466 oder x2 ≈ -0,284 sind mögliche Wendestellen.
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung f '''(x)≠ 0.
f '''(-1,466) = 48⋅(-1,466) + 42 < 0 → W1(-1,466/-2,07) ist Wendepunkt
f '''(-0,284) = 48⋅(-0,284) + 42 > 0 → W2(-0,284/0,256) ist Wendepunkt
6. Verhalten für sehr kleine und sehr große x:
$$\lim_{x \to -\infty} f(x)~=~+\infty ~~~~~~~~~\lim_{x \to +\infty} f(x)~=~+\infty$$
Wendetangenten bestimmen mit dem Ansatz t(x) = m ⋅ x + b:
für W1 (-1,466/-2,07):
Die Steigung m entspricht der Ableitung an der Wendestelle:
m = f '(x1) = f '(-1,466) = 8⋅(-1,466)3 + 21⋅(-1,466)2 + 10⋅(-1,466) ≈ 5,27
Um b zu berechnen, setzt man den Wendepunkt in die Tangentengleichung ein:
b = f(-1,466) - f '(-1,466) ⋅ (-1,466) ≈ -2,07 - 5,27 ⋅ (-1,466) ≈ 5,66
Insgesamt t1(x) = 5,27 ⋅ x + 5,66
Entsprechend für t2: m2 = f '(-0,284) ≈ -1,33 sowie b2 ≈ 0,256 - (-1,33) ⋅ (-0,284) ≈ -0,12
Insgesamt t2(x) = -1,33 ⋅ x - 0,12
Tangentengleichungen gleichsetzen: t1(x) = t2(x) → 5,27 ⋅ x + 5,66 = -1,33 ⋅ x - 0,12
Daraus folgt: xs ≈ -0,88
xs in eine Tangentengleichung einsetzen. t1(-0,88) = 5,27 ⋅ (-0,88) + 5,66 ≈ 1,02
Der Schnittpunkt der Wendetangente ist etwa (-0,88/1,02).
| a) f(x) = sin (x) ⋅ cos (x) | b) f(x) = |
| c) f(x) = tan ((2⋅x - 2)2) | d) f(x) = |
a) f '(x) = cos2x - sin2x
b) f '(x) = =
c) f '(x) =
d) f '(x) =
b) f '(x) = =
c) f '(x) =
d) f '(x) =
b) Eine Zündholzschachtel soll 5 cm lang sein und ein Volumen von 45 cm3 besitzen. Bei welcher Breite und welcher Höhe benötigt man am wenigsten Material?
zu a):
Sei ein Rechteck mit den Seitenlängen a und b (a,b > 0) gegeben.
Ansatz: Die Länge der Diagonalen d beträgt dann:
Hauptfunktion d(a,b) = (Minimum gesucht)
Mit Hilfe der Nebenbedingung wird eine Variable der Hauptfunktion ersetzt. Dann ist die Hauptbedingung nur noch von einer Variablen abhängig.
Nebenbedingung: Umfang u(a,b) = 2⋅a + 2⋅b = 30 → b = 15 - a
Einsetzen der Neben- in die Hauptbedingung führt zur
Zielfunktion: d(a) = =
Nun muss ein Extremwert ermittelt werden:
Notwendige Bedingung: d '(a) = 0 → d '(a) = 2 ⋅ (2⋅a2 - 30⋅a + 225)-0,5 ⋅ (4⋅a - 30) = 0
→ (4⋅a - 30) = 0 (die anderen Faktoren können nicht Null werden)
→ aE = 7,5
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung d ''(aE) ≠ 0.
Allerdings ist die Berechnung der 2. Ableitung von d recht aufwendig. Entweder man verzichtet auf die hinreichende Bedingung (aus Zeitgründen) oder alternativ schaut man, ob ein Vorzeichenwechsel am möglichen Extremwert vorliegt. Dann überprüft man etwa
d'(7) = 2 ⋅ (2⋅72 - 30⋅7 + 225)-0,5 ⋅ (4⋅7 - 30) ≈ -0,44 < 0 sowie
d'(8) = 2 ⋅ (2⋅82 - 30⋅8 + 225)-0,5 ⋅ (4⋅8 - 30) ≈ 0,38 > 0
Aus dem Vorzeichenwechsel von Minus zu Plus folgt ein relatives Minimum an der Stelle aE = 7,5.
Nun noch aE in die Hauptfunktion oder Zielfunktion sowie die Nebenbedingung einsetzen. Dann ist bE = 15 - 7,5 = 7,5 und d ≈ 10,61.
Antwort: Die kürzeste Diagonale eines Rechtecks mit dem Umfang 30 cm ist 10,61 cm lang. Dann ist das Rechteck ein Quadrat mit der Seitenlänge 7,5 cm.
zu b)
Nun soll die Oberfläche O der Zündholzschachtel minimiert werden. Die Schachtel ist ein Quader mit den Grundseiten a und b sowie der Höhe h (a,b,h > 0). Deshalb ist der Ansatz:
Hauptfunktion: Oberfläche O(a,b,h) = 2⋅a⋅b + 2⋅a⋅h + 2⋅b⋅h (gesucht: Minimum)
Nebenbedingungen: a = 5 sowie Volumen V(a,b,h) = a ⋅ b ⋅ h = 5 ⋅ b ⋅ h = 45 → b =
Einsetzen in die Hauptbedingung führt zur
Zielfunktion O(h) = 2⋅5⋅ + 2⋅5⋅h + 2⋅⋅h = + 10⋅h + 18
Extremwert ermitteln:
Notwendige Bedingung: O '(h) = 0 → O '(h) = - + 10 = 0 → hE = 3 (die Lösung h = -3 ist nicht sinnvoll)
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
O ''(hE) ≠ 0 mit O''(h) = .
O ''(hE) = > 0 → hE = 3 ist rel. Minimum.
Nun noch hE in die Hauptfunktion oder Zielfunktion sowie die Nebenbedingung einsetzen. Dann ist bE = = 3 und die minimale Oberfläche: O(a,b,h) = 2⋅5⋅3 + 2⋅5⋅3 + 2⋅3⋅3 = 78.
Antwort: Die minimale Oberfläche einer Zündholschachtel mit einem Volumen von 45 cm3 und einer Länge von 5 cm beträgt 78 cm2. Dann ist die Schachtel 3 cm breit und 3 cm hoch.
Sei ein Rechteck mit den Seitenlängen a und b (a,b > 0) gegeben.
Ansatz: Die Länge der Diagonalen d beträgt dann:
Hauptfunktion d(a,b) = (Minimum gesucht)
Mit Hilfe der Nebenbedingung wird eine Variable der Hauptfunktion ersetzt. Dann ist die Hauptbedingung nur noch von einer Variablen abhängig.
Nebenbedingung: Umfang u(a,b) = 2⋅a + 2⋅b = 30 → b = 15 - a
Einsetzen der Neben- in die Hauptbedingung führt zur
Zielfunktion: d(a) = =
Nun muss ein Extremwert ermittelt werden:
Notwendige Bedingung: d '(a) = 0 → d '(a) = 2 ⋅ (2⋅a2 - 30⋅a + 225)-0,5 ⋅ (4⋅a - 30) = 0
→ (4⋅a - 30) = 0 (die anderen Faktoren können nicht Null werden)
→ aE = 7,5
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung d ''(aE) ≠ 0.
Allerdings ist die Berechnung der 2. Ableitung von d recht aufwendig. Entweder man verzichtet auf die hinreichende Bedingung (aus Zeitgründen) oder alternativ schaut man, ob ein Vorzeichenwechsel am möglichen Extremwert vorliegt. Dann überprüft man etwa
d'(7) = 2 ⋅ (2⋅72 - 30⋅7 + 225)-0,5 ⋅ (4⋅7 - 30) ≈ -0,44 < 0 sowie
d'(8) = 2 ⋅ (2⋅82 - 30⋅8 + 225)-0,5 ⋅ (4⋅8 - 30) ≈ 0,38 > 0
Aus dem Vorzeichenwechsel von Minus zu Plus folgt ein relatives Minimum an der Stelle aE = 7,5.
Nun noch aE in die Hauptfunktion oder Zielfunktion sowie die Nebenbedingung einsetzen. Dann ist bE = 15 - 7,5 = 7,5 und d ≈ 10,61.
Antwort: Die kürzeste Diagonale eines Rechtecks mit dem Umfang 30 cm ist 10,61 cm lang. Dann ist das Rechteck ein Quadrat mit der Seitenlänge 7,5 cm.
zu b)
Nun soll die Oberfläche O der Zündholzschachtel minimiert werden. Die Schachtel ist ein Quader mit den Grundseiten a und b sowie der Höhe h (a,b,h > 0). Deshalb ist der Ansatz:
Hauptfunktion: Oberfläche O(a,b,h) = 2⋅a⋅b + 2⋅a⋅h + 2⋅b⋅h (gesucht: Minimum)
Nebenbedingungen: a = 5 sowie Volumen V(a,b,h) = a ⋅ b ⋅ h = 5 ⋅ b ⋅ h = 45 → b =
Einsetzen in die Hauptbedingung führt zur
Zielfunktion O(h) = 2⋅5⋅ + 2⋅5⋅h + 2⋅⋅h = + 10⋅h + 18
Extremwert ermitteln:
Notwendige Bedingung: O '(h) = 0 → O '(h) = - + 10 = 0 → hE = 3 (die Lösung h = -3 ist nicht sinnvoll)
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
O ''(hE) ≠ 0 mit O''(h) = .
O ''(hE) = > 0 → hE = 3 ist rel. Minimum.
Nun noch hE in die Hauptfunktion oder Zielfunktion sowie die Nebenbedingung einsetzen. Dann ist bE = = 3 und die minimale Oberfläche: O(a,b,h) = 2⋅5⋅3 + 2⋅5⋅3 + 2⋅3⋅3 = 78.
Antwort: Die minimale Oberfläche einer Zündholschachtel mit einem Volumen von 45 cm3 und einer Länge von 5 cm beträgt 78 cm2. Dann ist die Schachtel 3 cm breit und 3 cm hoch.
Die Tangente in P(-3/0) ist parallel zu der Geraden y = 6x.
b) Eine achsensymmetrische Parabel 4.Ordnung geht durch (0/2) und hat in (1/0) einen Tiefpunkt.
zu a)
Ansatz: f(x) = a3⋅x3 + a2⋅x2 + a1⋅x + a0 und daraus f '(x) = 3⋅a3⋅x2 + 2⋅a2⋅x + a1
Bedingungen:
I. f(0) = 0 → a3⋅03 + a2⋅02 + a1⋅0 + a0 = 0 → a0 = 0
II. f '(0) = 0 → 3⋅a3⋅02 + 2⋅a2⋅0 + a1 = 0 → a1 = 0
III. f '(-3) = 6 → 3⋅a3⋅(-3)2 + 2⋅a2⋅(-3) + a1 = 6 → 27⋅a3 - 6⋅a2⋅ + a1 = 6 → 27⋅a3 - 6⋅a2 = 6
IV. f(-3) = 0 → a3⋅(-3)3 + a2⋅(-3)2 + a1⋅(-3) + a0 = 0 → -27⋅a3 + 9⋅a2 - 3⋅a1 + a0 = 0 → -27⋅a3 + 9⋅a2 = 0
Zur Lösung des linearen Gleichungssystems können die einschlägig bekannten Verfahren (z.B. Additionsverfahren) verwendet werden - oder einen Taschenrechner bemühen.
Aus III. und IV. folgen a2 = 2 sowie a3 =
Die Zuordnungsvorschrift lautet: f(x) = ⋅x3 + 2⋅x2
zu b)
Ansatz: wegen der Achsensymmetrie nur gerade Exponenten, deshalb
f(x) = a4⋅x4 + a2⋅x2 + a0 und daraus f '(x) = 4⋅a4⋅x3 + 2⋅a2⋅x
Bedingungen:
I. f(0) = 2 → a4⋅04 + a2⋅02 + a0 = 2 → a0 = 2
II. f(1) = 0 → a4⋅14 + a2⋅12 + a0 = 0 → a4 + a2 + a0 = 0 → a4 + a2 = -2 (wegen I.)
III. f '(1) = 0 → 4⋅a4⋅13 + 2⋅a2⋅1 = 0 → 4⋅a4 + 2⋅a2 = 0
Zur Lösung des linearen Gleichungssystems können die einschlägig bekannten Verfahren (z.B. Additionsverfahren) verwendet werden - oder einen Taschenrechner bemühen.
Dann: a4 = 2 sowie a2 = -4
Die Zuordnungsvorschrift lautet: f(x) = 2⋅x4 - 4⋅x2 + 2
Ansatz: f(x) = a3⋅x3 + a2⋅x2 + a1⋅x + a0 und daraus f '(x) = 3⋅a3⋅x2 + 2⋅a2⋅x + a1
Bedingungen:
I. f(0) = 0 → a3⋅03 + a2⋅02 + a1⋅0 + a0 = 0 → a0 = 0
II. f '(0) = 0 → 3⋅a3⋅02 + 2⋅a2⋅0 + a1 = 0 → a1 = 0
III. f '(-3) = 6 → 3⋅a3⋅(-3)2 + 2⋅a2⋅(-3) + a1 = 6 → 27⋅a3 - 6⋅a2⋅ + a1 = 6 → 27⋅a3 - 6⋅a2 = 6
IV. f(-3) = 0 → a3⋅(-3)3 + a2⋅(-3)2 + a1⋅(-3) + a0 = 0 → -27⋅a3 + 9⋅a2 - 3⋅a1 + a0 = 0 → -27⋅a3 + 9⋅a2 = 0
Zur Lösung des linearen Gleichungssystems können die einschlägig bekannten Verfahren (z.B. Additionsverfahren) verwendet werden - oder einen Taschenrechner bemühen.
Aus III. und IV. folgen a2 = 2 sowie a3 =
Die Zuordnungsvorschrift lautet: f(x) = ⋅x3 + 2⋅x2
zu b)
Ansatz: wegen der Achsensymmetrie nur gerade Exponenten, deshalb
f(x) = a4⋅x4 + a2⋅x2 + a0 und daraus f '(x) = 4⋅a4⋅x3 + 2⋅a2⋅x
Bedingungen:
I. f(0) = 2 → a4⋅04 + a2⋅02 + a0 = 2 → a0 = 2
II. f(1) = 0 → a4⋅14 + a2⋅12 + a0 = 0 → a4 + a2 + a0 = 0 → a4 + a2 = -2 (wegen I.)
III. f '(1) = 0 → 4⋅a4⋅13 + 2⋅a2⋅1 = 0 → 4⋅a4 + 2⋅a2 = 0
Zur Lösung des linearen Gleichungssystems können die einschlägig bekannten Verfahren (z.B. Additionsverfahren) verwendet werden - oder einen Taschenrechner bemühen.
Dann: a4 = 2 sowie a2 = -4
Die Zuordnungsvorschrift lautet: f(x) = 2⋅x4 - 4⋅x2 + 2
a) Zeichnen Sie die Graphen von f-6 , f-4 , f-2, f0, f2 in ein Koordinatensystem.
b) Berechnen Sie die Schnittpunkte mit der x-Achse. Für welche Werte von k sind 2 Schnittpunkte vorhanden?
c) Ermitteln Sie das Minimum.
d) Zeigen Sie, dass alle Graphen durch den Punkt (1/1) gehen.
e) Für welchen Wert von k ist das Minimum von fk am größten?
f) Geben Sie die Ortskurve der Extrema an.
zu a)
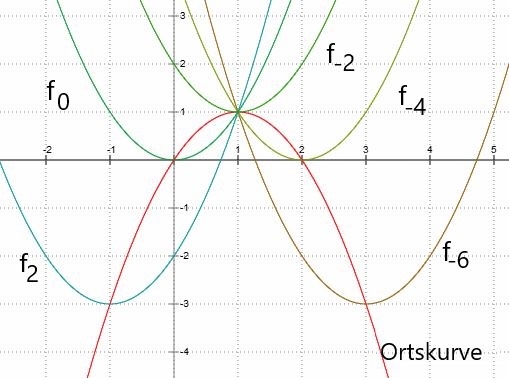
s. Zeichnung
zu b)
Ansatz: fk(xN) = 0 → xN2 + k⋅xN – k = 0 → xN = - ±
Es gibt 2 Nullstellen, falls der Radikand positiv ist.
Deshalb: + k > 0 → k ⋅ (k + 4) > 0
1. Fall: k > 0 und k + 4 > 0 → k > 0
2. Fall: k < 0 und k + 4 < 0 → k < - 4
Es gibt 2 Nullstellen, falls k > 0 oder k < - 4 ist.
zu c)
Notwendige Bedingung: fk'(x) = 2⋅x + k = 0 → xE = -
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
fk''(xE) ≠ 0 mit fk''(x) = 2.
fk''(xE) = fk''(-) = 2 > 0 → (- / - - k) ist rel. Minimum.
zu d)
Berechne fk(1) = 12 + k⋅1 – k = 1
Der Funktionswert an der Stelle x = 1 ist unabhängig von dem Parameter k. und beträgt 1. Deshalb besitzen alle Graphen der Funktionenschar den gemeinsamen Punkt (1/1).
zu e)
Der Funktionswert des Minimums beträgt - - k. Dieser Ausdruck ist von k abhängig und soll maximiert werden.
Hauptfunktion g(k) = - - k soll maximal werden
Notwendige Bedingung: g'(k) = -⋅k - 1 = 0 → kE = -2
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
g''(kE) ≠ 0 mit g''(k) = -.
g''(kE) = g''(-2) = - < 0 → (-2 / 1) ist rel. Maximum.
Das Minimum der Graphen der Funktionenschar wird für k = -2 maximal. Der größte Wert der Minima beträgt 1. (s. auch Graphik)
zu f)
Um die Ortskurve der Minima zu bestimmen, muss der Parameter k für die Minima (- / - - k) eliminiert werden.
Es gilt: xE = - → k = - 2⋅xE
Einsetzen in yE = - - k = - - (- 2⋅xE) = - xE2 + 2⋅xE.
Ortskurve der Minima: y(x) = - x2 + 2⋅x

s. Zeichnung
zu b)
Ansatz: fk(xN) = 0 → xN2 + k⋅xN – k = 0 → xN = - ±
Es gibt 2 Nullstellen, falls der Radikand positiv ist.
Deshalb: + k > 0 → k ⋅ (k + 4) > 0
1. Fall: k > 0 und k + 4 > 0 → k > 0
2. Fall: k < 0 und k + 4 < 0 → k < - 4
Es gibt 2 Nullstellen, falls k > 0 oder k < - 4 ist.
zu c)
Notwendige Bedingung: fk'(x) = 2⋅x + k = 0 → xE = -
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
fk''(xE) ≠ 0 mit fk''(x) = 2.
fk''(xE) = fk''(-) = 2 > 0 → (- / - - k) ist rel. Minimum.
zu d)
Berechne fk(1) = 12 + k⋅1 – k = 1
Der Funktionswert an der Stelle x = 1 ist unabhängig von dem Parameter k. und beträgt 1. Deshalb besitzen alle Graphen der Funktionenschar den gemeinsamen Punkt (1/1).
zu e)
Der Funktionswert des Minimums beträgt - - k. Dieser Ausdruck ist von k abhängig und soll maximiert werden.
Hauptfunktion g(k) = - - k soll maximal werden
Notwendige Bedingung: g'(k) = -⋅k - 1 = 0 → kE = -2
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
g''(kE) ≠ 0 mit g''(k) = -.
g''(kE) = g''(-2) = - < 0 → (-2 / 1) ist rel. Maximum.
Das Minimum der Graphen der Funktionenschar wird für k = -2 maximal. Der größte Wert der Minima beträgt 1. (s. auch Graphik)
zu f)
Um die Ortskurve der Minima zu bestimmen, muss der Parameter k für die Minima (- / - - k) eliminiert werden.
Es gilt: xE = - → k = - 2⋅xE
Einsetzen in yE = - - k = - - (- 2⋅xE) = - xE2 + 2⋅xE.
Ortskurve der Minima: y(x) = - x2 + 2⋅x
 1. Ableitungen:
1. Ableitungen: fa'(x) = 3⋅x2 - 6⋅a⋅x - 1 fa''(x) = 6⋅x - 6⋅a fa'''(x) = 6
2. Symmetrie:
Die Funktion ist weder punkt- noch achsensymmetrisch, denn f ist eine ganzrationale Funktion mit geraden und ungeraden Exponenten. Ausnahme: Für a = 0 ist die Funktion punktsymmtrisch (nur ungerade Exponenten).
3. Schnittpunkte mit den Achsen:
Schnittpunkt mit der x-Achse sind Nullstellen:
Ansatz: f(x) = 0
1. Nullstelle raten: xN1 = 3⋅a
Polynomdivision: (x3 – 3⋅a⋅x2 - x + 3⋅a) : (x - 3⋅a) = x2 -1
Weiter: x2 -1 = 0 → xN2 = -1 und xN3 = 1
Insgesamt: Nullstellen sind N1 (3⋅a/0) , N2 (-1/0) sowie N3 (1/0)
Schnittpunkt mit der y-Achse: f(0) = 3⋅a → (0/3⋅a) ist der Schnittpunkt des Graphen von f mit der y-Achse
4. Extremwerte.
Notwendige Bedingung: fa'(x) = 0 → fa'(x) = 3⋅x2 - 6⋅a⋅x - 1 = 0 → xE1,2 = a ±
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die
hinreichende Bedingung fa''(x) = 6⋅x - 6⋅a ≠ 0:
fa ''(a - ) = 6⋅(a - ) - 6⋅a = -6⋅ < 0 → E1 ( a - / fa(xE1) ) rel. Maximum.
fa ''(a + ) = 6⋅(a + ) - 6⋅a = 6⋅ > 0 → E2 ( a + / fa(xE2) ) rel. Minimum.
5. Wendepunkte:
Notwendige Bedingung: fa''(x) = 0 → fa''(x) = 6⋅x - 6⋅a = 0 → xW = a
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung fa'''(xW)≠ 0.
fa'''(a) = 6 > 0 → W(a/-2⋅a3 + 2⋅a) ist Wendepunkt.
6. Verhalten für sehr kleine und sehr große x:
$$\lim_{x \to -\infty} f(x)~=~-\infty ~~~~~~~~~\lim_{x \to +\infty} f(x)~=~+\infty$$
Baulöwe Willi will ein Hochhaus errichten. Bauplatz- und Planungskosten werden mit 2 Mio Euro veranschlagt, das Erdgeschoss mit 200000 Euro. Jede weitere Etage wird 10000 Euro mehr kosten als die vorangehende. Jede Etage wird 10000 Euro Miete einbringen. Wie viele Etagen wird er bauen, um ein möglichst günstiges Verhältnis der Baukosten zu den Mieteinnahmen zu erzielen?
Sei n die Anzahl der Stockwerke (auch das Erdgeschoss ist ein Stockwerk) mit n ≥ 1.
Die Mieteinnahmen m betragen in 10000 €: m(n) = n.
Die Baukosten k betragen
k(n) = 200 + (20+0) + (20+1) + (20+2) + ... + (20+(n-1)) = 200 + 20⋅n + i = 200 + 20⋅n+
Das Verhältnis v der Baukosten k zu Mieteinahmen m ist: v = . v soll minimiert werden.
Hauptfunktion: v(n) = = + 19,5 + ⋅n (soll minimiert werden)
Extremwert ermitteln:
Notwendige Bedingung: v'(n) = 0 → v'(n) = - + = 0 → nE = 20 (die Lösung n = -20 ist nicht sinnvoll)
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
v ''(nE) ≠ 0 mit v''(n) = .
v ''(nE) = > 0 → (20 / 39,5) ist rel. Minimum.
Das Verhältnis von Baukosten zu Mieteinnahmen ist für 20 Stockwerke am günstigsten. Das Verhältnis beträgt dann 39,5, d.h. nach 39,5 Monaten hätte sich das Projekt amortisiert, wenn man Betriebskosten außer Acht lässt.
Die Mieteinnahmen m betragen in 10000 €: m(n) = n.
Die Baukosten k betragen
k(n) = 200 + (20+0) + (20+1) + (20+2) + ... + (20+(n-1)) = 200 + 20⋅n + i = 200 + 20⋅n+
Das Verhältnis v der Baukosten k zu Mieteinahmen m ist: v = . v soll minimiert werden.
Hauptfunktion: v(n) = = + 19,5 + ⋅n (soll minimiert werden)
Extremwert ermitteln:
Notwendige Bedingung: v'(n) = 0 → v'(n) = - + = 0 → nE = 20 (die Lösung n = -20 ist nicht sinnvoll)
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
v ''(nE) ≠ 0 mit v''(n) = .
v ''(nE) = > 0 → (20 / 39,5) ist rel. Minimum.
Das Verhältnis von Baukosten zu Mieteinnahmen ist für 20 Stockwerke am günstigsten. Das Verhältnis beträgt dann 39,5, d.h. nach 39,5 Monaten hätte sich das Projekt amortisiert, wenn man Betriebskosten außer Acht lässt.
a) Die untere linke Ecke liegt im Ursprung des Koordinatensystems. Fertigen Sie eine Zeichnung an und zeigen Sie, dass sich die Diagonale durch die Funktion f(x) = -0,4 x + 2 beschreiben lässt.
b) Aus der verbleibenden (dreieckigen) Glasplatte soll eine möglichst große rechteckige Glasscheibe ausgeschnitten werden. Dabei liegt eine Ecke auf der Hypotenuse. Bestimmen Sie diesen maximalen Flächeninhalt.
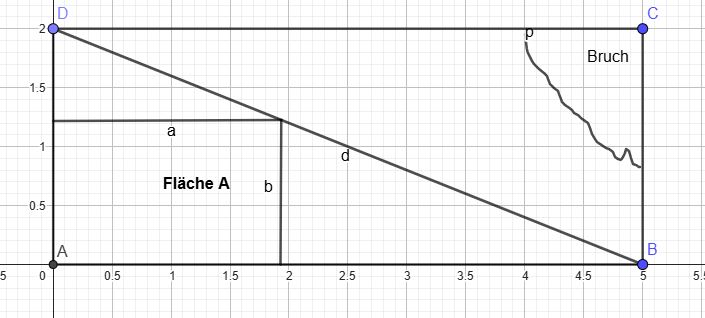 zu a)
zu a)Ansatz für die Diagonale: d(x) = m⋅x + b Verlauf durch die Punkte D(0/2) und B(5/0)
Dann: Steigung m = = = - = - 0,4
Der y-Achsenabschnitt b ist direkt ablesbar (wegen Punkt D): b = 2 → d(x) = -0,4⋅x + 2
zu b)
Hauptfunktion Fläche A(a,b) = a ⋅ b maximieren
Nebenbedingung: b = - 0,4⋅a + 2
Einsetzen in die Hauptfunktion führt zur
Zielfunktion: A(a) = a ⋅ (- 0,4⋅a + 2) = - 0,4 a2 + 2⋅ a
Extremwert ermitteln:
Notwendige Bedingung: A'(a) = 0 → A'(a) = - 0,8⋅a + 2 = 0 → aE = 2,5
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung
A ''(aE) ≠ 0 mit A''(a) = - 0,8.
A ''(aE) = - 0,8 < 0 → aE = 2,5 ist rel. Maximum.
Nun noch aE in die Hauptfunktion oder Zielfunktion sowie die Nebenbedingung einsetzen.
Dann ist bE = - 0,4 ⋅ 2,5 + 2 = 1 und die maximale Fläche: A(a,b) = 2,5 ⋅ 1 = 2,5.
Antwort: Die maximale Fläche beträgt 2,5 m2 bei einer Länge von 2,5 m und einer Breite von 1 m.
(Anmerkung: Nebenbedingung mit Strahlensatz ab Punkt ((0/y))
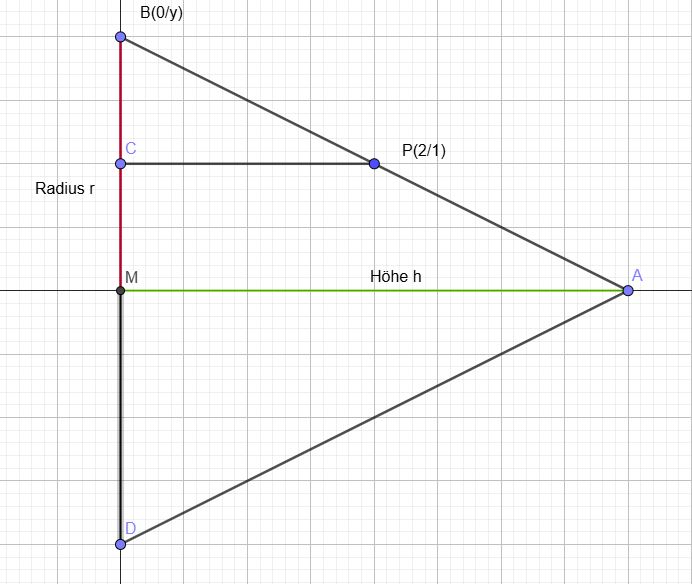 Ansatz mit Volumen eines Kegels mit Radius r > 0 sowie Höhe h >0:
Ansatz mit Volumen eines Kegels mit Radius r > 0 sowie Höhe h >0: V(r,h) = ⋅π⋅r2⋅h soll minimiert werden.
Nebenbedingung mit Strahlensatz (Zentrum B):
= → = → h =
Einsetzen in die Hauptfunktion führt zur
Zielfunktion: V(r) = ⋅π⋅r2⋅ = ⋅π⋅
Extremwert ermitteln:
Notwendige Bedingung: V '(r) = 0 → V '(r) = ⋅π⋅ = 0
→ 2⋅r3 - 3⋅r2 = r2⋅(2⋅r - 3) = 0 → rE1 = 0 oder rE2 = 1,5
Nur rE2 sinnvoll
Falls die notwendige Bedingung erfüllt ist, genügt als Überprüfung die hinreichende Bedingung mit Vorzeichenwechsel für die 1. Ableitung (Bildung 2. Ableitung ist aufwendig).
V '(1,4) = ⋅π⋅ < 0
V '(2) = ⋅π⋅ > 0
→ an der Stelle rE2 liegt ein relatives Minimum vor. Nun noch rE2 in die Hauptfunktion oder Zielfunktion sowie die Nebenbedingung einsetzen.
Dann ist hE = = 6 und das maximale Volumen: V(r,h) = ⋅π⋅1,52⋅6 = 4,5.
Antwort: Das maximale Volumen des Kegels beträgt 4,5 Volumeneinheiten bei einem Radius von 1,5 Längeneinheiten und einer Höhe von 6 Längeneinheiten.