die Kugel K: \( \left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right) ^2 = 25 \) und die Ebene E: \( \begin{pmatrix}1\\5\\9 \end{pmatrix} \cdot \left(\vec{x}-\begin{pmatrix}2\\3\\1 \end{pmatrix}\right) = 0 \).
a) Geben Sie die Lage von B bezüglich der Kugel an. Zeigen Sie, dass A auf der Kugel liegt.
b) Bestimmen Sie den Schnittkreis zwischen der Ebene E und der Kugel K.
c) Geben Sie die Gleichung der Tangentialebene T im Punkt A an die Kugel an. Ermitteln Sie die zu T parallele Tangentialebene T´ an die Kugel K.
d) Wie groß ist die kleinste bzw. größte Entfernung eines Kugelpunktes vom Mittelpunkt des Schnittkreises?
zu a)
Punkte in die Kugelgleichung einsetzen:
B einsetzen: \( \left(\begin{pmatrix}3\\6\\2 \end{pmatrix} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right) ^2 = \begin{pmatrix}4\\3\\-3\end{pmatrix} ^2 =4^2+3^2+(-3)^2 = 34 > 25\)
B liegt außerhalb der Kugel K.
A einsetzen: \( \left(\begin{pmatrix}2\\3\\9 \end{pmatrix} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right) ^2 = \begin{pmatrix}3\\0\\4 \end{pmatrix} ^2 =3^2+0^2+4^2 = 25\)
A erfüllt die Kugelgleichung → A ∈ K.
zu b)
Es ist der Mittelpunkt MS und der Radius rS des Schnittkreises zu bestimmen.
Der Mittelpunkt MS ist der Schnittpunkt der Ebene E mit der zu E orthogonalen Geraden g durch den Mittelpunkt M der Kugel.
g: \(\vec{r}= \begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 5 \\ 9 \end{pmatrix}\)
Nun g in die Normalenform von E einsetzen:
\(\begin{pmatrix} 1 \\ 5 \\ 9 \end{pmatrix}\cdot \left(\begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 5 \\ 9 \end{pmatrix}- \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}\right)=0\) \(~\rightarrow~59+107\lambda-26=0\) \(~\rightarrow ~\lambda=-\frac{33}{107}\)
λ in g einsetzen:
\(\vec{f}= \begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix} - \frac{33}{107}\cdot \begin{pmatrix} 1 \\ 5 \\ 9 \end{pmatrix}\) → MS(\(-\frac{140}{107}\)/\(\frac{156}{107}\)/\(\frac{238}{107}\))
Der Radius rS des Schnittkreises wird bestimmt mit dem Satz des Pythagoras: rS = \(\sqrt{r^2-|MM_S|^2}\)
mit r = 5 sowie MMS = \(\sqrt{(-\frac{140}{107}+1)^2+(\frac{156}{107}-3)^2+(\frac{238}{107}-5)^2}=\frac{\sqrt{116523}}{107}\approx3,19\)
Daraus folgt rS = \(\sqrt{r^2-|MM_S|^2}=\sqrt{25-\frac{116523}{107^2}}\approx3,85\)
zu c)
Die Gleichung der Tangentialebene T an eine Kugel K (mit Mittelpunkt M und Radius r) im Berührpunkt B lautet:
T: \((\vec{x}-\vec{m})\cdot(\vec{b}-\vec{m})=r^2\)
Durch Einsetzen erhält man T: \(\left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)\cdot\left(\begin{pmatrix}2\\3\\9 \end{pmatrix} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)=25\)
Zusammenfassen: T: \(\left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)\cdot\begin{pmatrix}3\\0\\4 \end{pmatrix}=25\) oder T: \(\begin{pmatrix}3\\0\\4 \end{pmatrix}\cdot\vec{x}-42=0\)
Zum Berührpunkt A' der parallelen Tangentialebene T' gelangt man durch
\(\vec{a'}=\vec{m}+\vec{AM}=\begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix}+\begin{pmatrix} -3 \\ 0 \\ -4 \end{pmatrix}=\begin{pmatrix} -4 \\ 3 \\ 1 \end{pmatrix}\)
Nun wieder in die Gleichung einer Tangentialebene einsetzen:
T': \(\left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)\cdot\left(\begin{pmatrix}-4\\3\\1 \end{pmatrix} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)=25\)
Zusammenfassen: T': \(\left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)\cdot\begin{pmatrix}-3\\0\\-4 \end{pmatrix}=25\) oder T': \(\begin{pmatrix}3\\0\\4 \end{pmatrix}\cdot\vec{x}+8=0\)
Anmerkung: Mit Hilfe der Hesse-Form der Tangentialgleichungen (einfach jeweils durch den Betrag des Normalenvektors - also 5 - dividieren) erkennt man, dass die Tangentialebene T den Abstand \(\frac{42}{5}\) und die Tangentialebene T' den Abstand \(\frac{8}{5}\) vom Ursprung besitzen, aber auf verschiedenen Seiten des Ursprungs (zu erkennen an den unterschiedlichen Vorzeichen). Insgesamt besitzen sie demnach den Abstand 10 voneinander. Das entspricht gerade dem doppelten Raius der Kugel. So wurde schließlich A' auch konstruiert.
zu d)
Die maximale Entfernung beträgt r + |\(\vec{MM_S}\)| ≈ 8,19 LE.
Die minimale Entfernung beträgt r - |\(\vec{MM_S}\)| ≈ 1,81 LE.
Punkte in die Kugelgleichung einsetzen:
B einsetzen: \( \left(\begin{pmatrix}3\\6\\2 \end{pmatrix} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right) ^2 = \begin{pmatrix}4\\3\\-3\end{pmatrix} ^2 =4^2+3^2+(-3)^2 = 34 > 25\)
B liegt außerhalb der Kugel K.
A einsetzen: \( \left(\begin{pmatrix}2\\3\\9 \end{pmatrix} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right) ^2 = \begin{pmatrix}3\\0\\4 \end{pmatrix} ^2 =3^2+0^2+4^2 = 25\)
A erfüllt die Kugelgleichung → A ∈ K.
zu b)
Es ist der Mittelpunkt MS und der Radius rS des Schnittkreises zu bestimmen.
Der Mittelpunkt MS ist der Schnittpunkt der Ebene E mit der zu E orthogonalen Geraden g durch den Mittelpunkt M der Kugel.
g: \(\vec{r}= \begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 5 \\ 9 \end{pmatrix}\)
Nun g in die Normalenform von E einsetzen:
\(\begin{pmatrix} 1 \\ 5 \\ 9 \end{pmatrix}\cdot \left(\begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\ 5 \\ 9 \end{pmatrix}- \begin{pmatrix} 2 \\ 3 \\ 1 \end{pmatrix}\right)=0\) \(~\rightarrow~59+107\lambda-26=0\) \(~\rightarrow ~\lambda=-\frac{33}{107}\)
λ in g einsetzen:
\(\vec{f}= \begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix} - \frac{33}{107}\cdot \begin{pmatrix} 1 \\ 5 \\ 9 \end{pmatrix}\) → MS(\(-\frac{140}{107}\)/\(\frac{156}{107}\)/\(\frac{238}{107}\))
Der Radius rS des Schnittkreises wird bestimmt mit dem Satz des Pythagoras: rS = \(\sqrt{r^2-|MM_S|^2}\)
mit r = 5 sowie MMS = \(\sqrt{(-\frac{140}{107}+1)^2+(\frac{156}{107}-3)^2+(\frac{238}{107}-5)^2}=\frac{\sqrt{116523}}{107}\approx3,19\)
Daraus folgt rS = \(\sqrt{r^2-|MM_S|^2}=\sqrt{25-\frac{116523}{107^2}}\approx3,85\)
zu c)
Die Gleichung der Tangentialebene T an eine Kugel K (mit Mittelpunkt M und Radius r) im Berührpunkt B lautet:
T: \((\vec{x}-\vec{m})\cdot(\vec{b}-\vec{m})=r^2\)
Durch Einsetzen erhält man T: \(\left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)\cdot\left(\begin{pmatrix}2\\3\\9 \end{pmatrix} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)=25\)
Zusammenfassen: T: \(\left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)\cdot\begin{pmatrix}3\\0\\4 \end{pmatrix}=25\) oder T: \(\begin{pmatrix}3\\0\\4 \end{pmatrix}\cdot\vec{x}-42=0\)
Zum Berührpunkt A' der parallelen Tangentialebene T' gelangt man durch
\(\vec{a'}=\vec{m}+\vec{AM}=\begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix}+\begin{pmatrix} -3 \\ 0 \\ -4 \end{pmatrix}=\begin{pmatrix} -4 \\ 3 \\ 1 \end{pmatrix}\)
Nun wieder in die Gleichung einer Tangentialebene einsetzen:
T': \(\left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)\cdot\left(\begin{pmatrix}-4\\3\\1 \end{pmatrix} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)=25\)
Zusammenfassen: T': \(\left(\vec{x} - \begin{pmatrix}-1\\3\\5 \end{pmatrix} \right)\cdot\begin{pmatrix}-3\\0\\-4 \end{pmatrix}=25\) oder T': \(\begin{pmatrix}3\\0\\4 \end{pmatrix}\cdot\vec{x}+8=0\)
Anmerkung: Mit Hilfe der Hesse-Form der Tangentialgleichungen (einfach jeweils durch den Betrag des Normalenvektors - also 5 - dividieren) erkennt man, dass die Tangentialebene T den Abstand \(\frac{42}{5}\) und die Tangentialebene T' den Abstand \(\frac{8}{5}\) vom Ursprung besitzen, aber auf verschiedenen Seiten des Ursprungs (zu erkennen an den unterschiedlichen Vorzeichen). Insgesamt besitzen sie demnach den Abstand 10 voneinander. Das entspricht gerade dem doppelten Raius der Kugel. So wurde schließlich A' auch konstruiert.
zu d)
Die maximale Entfernung beträgt r + |\(\vec{MM_S}\)| ≈ 8,19 LE.
Die minimale Entfernung beträgt r - |\(\vec{MM_S}\)| ≈ 1,81 LE.
a) Zeigen Sie, dass das Dreieck ABC einen rechten Winkel besitzt.
b) Bestimmen Sie eine Gleichung der durch die Punkte A, B und C bestimmten Ebene E in Normalenform.
(mögliche Lösung für E: 2x1 + x2 + 2x3 - 2 = 0)
c) Die Gerade g ist gegeben durch die Punkte D(2/4/2) und F(3/6/2). Untersuchen Sie die gegenseitige Lage von g und E.
d) Eine Kugel K mit dem Radius r = 3 berühre die Ebene E im Punkt A. Bestimmen Sie mögliche Mittelpunkte der Kugel.
[Ein mögliches Ergebnis M1 (2/-3/5)]
e) Vom Punkt D aus wird ein Tangentialkegel an die Kugel K mit dem Radius r = 3 und dem Mittelpunkt M1 gelegt. Bestimmen Sie sein Volumen.
zu a)
\(\vec{AB}=\begin{pmatrix} 1 \\ 8\\ -5 \end{pmatrix}~~~~~~~~\vec{AC}=\begin{pmatrix} -2 \\ 8 \\ -2 \end{pmatrix}~~~~~~~~\vec{BC}=\begin{pmatrix} -3 \\ 0 \\ 3 \end{pmatrix}\)
\(\vec{AC}\cdot\vec{BC}=\begin{pmatrix} -2 \\ 8 \\ -2 \end{pmatrix}\cdot\begin{pmatrix} -3 \\ 0 \\ 3 \end{pmatrix}=6+0-6=0~\rightarrow~\vec{AC}\perp\vec{BC}\)
zu b)
Ebene E in Punktrichtungsform:
E: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~+~\mu\cdot(\vec{c}-\vec{a})~~\)
E: \(\vec{r}~=~\begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 8\\ -5 \end{pmatrix}~+~\mu \cdot \begin{pmatrix} -2 \\ 8 \\ -2 \end{pmatrix}\)
Ebene E in Normalenform: \(\vec{n}\cdot (\vec{r}-\vec{a})=0 \) mit
Normalenvektor \(\vec{n'}=\begin{pmatrix} 1 \\ 8 \\ -5 \end{pmatrix} \times \begin{pmatrix} -2 \\ 8 \\ -2 \end{pmatrix}= \begin{pmatrix} 24 \\ 12 \\ 24 \end{pmatrix} \)\(~\rightarrow~\vec{n}=\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}\)
Und daraus E: \(\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}\cdot \left(\vec{r}- \begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix}\right)=0\)
oder in Koordinatenform E: 2x1 + x1 + 2x3 - 2 = 0
zu c)
Mit der 2-Punkte -Form folgt: g: \( \vec{r}~=~ \vec{d}~+~\lambda\cdot(\vec{f}-\vec{d})~\)\(~\rightarrow~~\vec{r}~=~\begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} \)
Determinante der Spannvektoren und des Richtungsvektor bestimmen:
det(\(\vec{AB},\vec{AC},\vec{DF}\)) = 48 ≠ 0 → g und E schneiden sich.
zu d)
Zum Ortsvektor des Punktes A wird die dreifache Länge des Normaleneinheitsvektors von E addiert oder subtrahiert.
\(\vec{m_1}=\vec{a}+3\cdot\frac{1}{3}\cdot\vec{n^0}=\begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix}+3\cdot\frac{1}{3}\cdot\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix}\)\(~\rightarrow~M_1(2/-3/5)\)
\(\vec{m_2}=\vec{a}-3\cdot\frac{1}{3}\cdot\vec{n^0}=\begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix}-3\cdot\frac{1}{3}\cdot\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} -2 \\ -5 \\ 1 \end{pmatrix}\)\(~\rightarrow~M_1(-2/-5/1)\)
zu e)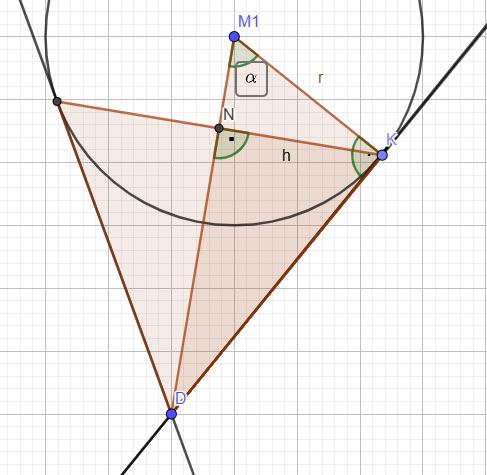
K ist ein Berührpunkt des Kegels an die Kugel. Die Höhe h des Dreiecks DKM1 entspricht dem Radius der Grundfläche des Tangentialkegels. Die Höhe des Tangentialkegels entspricht dem Abstand der Punkte N und D.
Das Dreieck DKM1 ist rechtwinklig aufgrund der Tangentialkonstruktion.
Der Tangentialkegel berührt die Kugel in einem Kreis.
Dieser Kreis ist der Schnittkreis der Kugel mit der Ebene T: \((\vec{x}-\vec{m_1})\cdot(\vec{d}-\vec{m_1})=r^2\)
Es gilt: T: \(\left(\vec{x} - \begin{pmatrix}2\\-3\\5 \end{pmatrix} \right)\cdot\left(\begin{pmatrix}2\\4\\2 \end{pmatrix} - \begin{pmatrix}2\\-3\\5 \end{pmatrix} \right)=9\)
Zusammenfassen: T: \(\left(\vec{x} - \begin{pmatrix}2\\-3\\5 \end{pmatrix} \right)\cdot\begin{pmatrix}0\\7\\-3 \end{pmatrix}=9\) oder
T: \(\begin{pmatrix}0\\7\\-3 \end{pmatrix}\cdot\vec{x}+27=0\)
N ist der Schnittpunkt der Ebene T mit der zu T orthogonalen Geraden h durch D (bzw. M1).
h: \( \vec{r}~=~ \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 0 \\ 7 \\ -3 \end{pmatrix} \)
h in T einsetzen:
\(\begin{pmatrix} 0 \\ 7 \\ -3 \end{pmatrix}\cdot \left(\begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} + \lambda \begin{pmatrix} 0 \\ 7 \\ -3 \end{pmatrix}\right)+27=0\) \(~\rightarrow~22+58\lambda+27=0\) \(~\rightarrow ~\lambda=-\frac{49}{58}\)
λ in h einsetzen:
\(\vec{f}= \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} -\frac{49}{58}\cdot \begin{pmatrix} 0 \\ 7 \\ -3 \end{pmatrix}\) \(~\rightarrow~N(2/-\frac{111}{58}/\frac{263}{58})\)
Höhe des Tangentialkegels hK = |\(\vec{DN}\)| = \(\left|\frac{1}{58}\cdot \begin{pmatrix} 0 \\ -343 \\ 147 \end{pmatrix}\right|\approx 6,43\)
Es gilt: |\(\vec{DM_1}\)| = \(\left|\begin{pmatrix} 0 \\ -7 \\ 3 \end{pmatrix}\right|=\sqrt{58}\approx 7,62\)
Daraus folgt: |\(\vec{NM_1}\)| ≈ 7,62 - 6,43 = 1,19.
Mit dem Höhensatz des Euklid lässt sich nun leicht die Höhe h berechnen: h = \(\sqrt{\vec{NM_1}\cdot\vec{DN}} \approx 2,77\).
Daraus erhält man für das Volumen des Tangentialkegels:
V = \(\frac{1}{3}\)⋅2,772⋅6,43 ≈ 16,4 VE.
\(\vec{AB}=\begin{pmatrix} 1 \\ 8\\ -5 \end{pmatrix}~~~~~~~~\vec{AC}=\begin{pmatrix} -2 \\ 8 \\ -2 \end{pmatrix}~~~~~~~~\vec{BC}=\begin{pmatrix} -3 \\ 0 \\ 3 \end{pmatrix}\)
\(\vec{AC}\cdot\vec{BC}=\begin{pmatrix} -2 \\ 8 \\ -2 \end{pmatrix}\cdot\begin{pmatrix} -3 \\ 0 \\ 3 \end{pmatrix}=6+0-6=0~\rightarrow~\vec{AC}\perp\vec{BC}\)
zu b)
Ebene E in Punktrichtungsform:
E: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~+~\mu\cdot(\vec{c}-\vec{a})~~\)
E: \(\vec{r}~=~\begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 8\\ -5 \end{pmatrix}~+~\mu \cdot \begin{pmatrix} -2 \\ 8 \\ -2 \end{pmatrix}\)
Ebene E in Normalenform: \(\vec{n}\cdot (\vec{r}-\vec{a})=0 \) mit
Normalenvektor \(\vec{n'}=\begin{pmatrix} 1 \\ 8 \\ -5 \end{pmatrix} \times \begin{pmatrix} -2 \\ 8 \\ -2 \end{pmatrix}= \begin{pmatrix} 24 \\ 12 \\ 24 \end{pmatrix} \)\(~\rightarrow~\vec{n}=\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}\)
Und daraus E: \(\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}\cdot \left(\vec{r}- \begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix}\right)=0\)
oder in Koordinatenform E: 2x1 + x1 + 2x3 - 2 = 0
zu c)
Mit der 2-Punkte -Form folgt: g: \( \vec{r}~=~ \vec{d}~+~\lambda\cdot(\vec{f}-\vec{d})~\)\(~\rightarrow~~\vec{r}~=~\begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} \)
Determinante der Spannvektoren und des Richtungsvektor bestimmen:
det(\(\vec{AB},\vec{AC},\vec{DF}\)) = 48 ≠ 0 → g und E schneiden sich.
zu d)
Zum Ortsvektor des Punktes A wird die dreifache Länge des Normaleneinheitsvektors von E addiert oder subtrahiert.
\(\vec{m_1}=\vec{a}+3\cdot\frac{1}{3}\cdot\vec{n^0}=\begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix}+3\cdot\frac{1}{3}\cdot\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix}\)\(~\rightarrow~M_1(2/-3/5)\)
\(\vec{m_2}=\vec{a}-3\cdot\frac{1}{3}\cdot\vec{n^0}=\begin{pmatrix} 0 \\ -4 \\ 3 \end{pmatrix}-3\cdot\frac{1}{3}\cdot\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} -2 \\ -5 \\ 1 \end{pmatrix}\)\(~\rightarrow~M_1(-2/-5/1)\)
zu e)

K ist ein Berührpunkt des Kegels an die Kugel. Die Höhe h des Dreiecks DKM1 entspricht dem Radius der Grundfläche des Tangentialkegels. Die Höhe des Tangentialkegels entspricht dem Abstand der Punkte N und D.
Das Dreieck DKM1 ist rechtwinklig aufgrund der Tangentialkonstruktion.
Der Tangentialkegel berührt die Kugel in einem Kreis.
Dieser Kreis ist der Schnittkreis der Kugel mit der Ebene T: \((\vec{x}-\vec{m_1})\cdot(\vec{d}-\vec{m_1})=r^2\)
Es gilt: T: \(\left(\vec{x} - \begin{pmatrix}2\\-3\\5 \end{pmatrix} \right)\cdot\left(\begin{pmatrix}2\\4\\2 \end{pmatrix} - \begin{pmatrix}2\\-3\\5 \end{pmatrix} \right)=9\)
Zusammenfassen: T: \(\left(\vec{x} - \begin{pmatrix}2\\-3\\5 \end{pmatrix} \right)\cdot\begin{pmatrix}0\\7\\-3 \end{pmatrix}=9\) oder
T: \(\begin{pmatrix}0\\7\\-3 \end{pmatrix}\cdot\vec{x}+27=0\)
N ist der Schnittpunkt der Ebene T mit der zu T orthogonalen Geraden h durch D (bzw. M1).
h: \( \vec{r}~=~ \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 0 \\ 7 \\ -3 \end{pmatrix} \)
h in T einsetzen:
\(\begin{pmatrix} 0 \\ 7 \\ -3 \end{pmatrix}\cdot \left(\begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} + \lambda \begin{pmatrix} 0 \\ 7 \\ -3 \end{pmatrix}\right)+27=0\) \(~\rightarrow~22+58\lambda+27=0\) \(~\rightarrow ~\lambda=-\frac{49}{58}\)
λ in h einsetzen:
\(\vec{f}= \begin{pmatrix} 2 \\ 4 \\ 2 \end{pmatrix} -\frac{49}{58}\cdot \begin{pmatrix} 0 \\ 7 \\ -3 \end{pmatrix}\) \(~\rightarrow~N(2/-\frac{111}{58}/\frac{263}{58})\)
Höhe des Tangentialkegels hK = |\(\vec{DN}\)| = \(\left|\frac{1}{58}\cdot \begin{pmatrix} 0 \\ -343 \\ 147 \end{pmatrix}\right|\approx 6,43\)
Es gilt: |\(\vec{DM_1}\)| = \(\left|\begin{pmatrix} 0 \\ -7 \\ 3 \end{pmatrix}\right|=\sqrt{58}\approx 7,62\)
Daraus folgt: |\(\vec{NM_1}\)| ≈ 7,62 - 6,43 = 1,19.
Mit dem Höhensatz des Euklid lässt sich nun leicht die Höhe h berechnen: h = \(\sqrt{\vec{NM_1}\cdot\vec{DN}} \approx 2,77\).
Daraus erhält man für das Volumen des Tangentialkegels:
V = \(\frac{1}{3}\)⋅2,772⋅6,43 ≈ 16,4 VE.
s. Üb-Geometrie