Mittelwerte


Mittelwerte dienen dazu, aus einer Gesamtheit von Werten einen sinnvollen durchschnittlichen Wert anzugeben. Nur - was soll ein sinnvoller durchschnittlicher Wert sein? Das hängt hauptsächlich vom Kontext der vorliegenden Daten ab.
Die bekanntesten Mittelwerte sind das arithmetische Mittel \(\overline{x}_a\) sowie der Median (oder Zentralwert) m.

Der Median m ist derjenige Wert, der genau 'in der Mitte' der nach Größe sortierten Werte steht. Bei einer geraden Anzahl an Werten ist der Median das arithmetisch Mittel der beiden mittleren Werte.
Das arithmetische Mittel ist definiert als die Summe der Werte dividiert durch ihre Anzahl: \(\overline{x}_a\) = 1n ∑ i=1 n xi

Beispiel 1:
Das Beispiel möge illustrieren, dass mit der Wahl eines dieser Mittelwerte durchaus (trotz mathematisch korrekter Berechnung) unterschiedliche Aussagen getroffen werden können.
Gegeben seien die Einkommen in 1000 € von 5 Personen in einem und im Folgejahr und daraus das arithmetische Mittel und der Median:

Person I II III IV V \(\overline{x}_a\) m
1. Jahr 50 60 60 80 200 90 60
2. Jahr 55 65 70 90 100 76 70


Man erkennt: Legt man den Median zugrunde, sind die Einkommen gestiegen. Legt man das arithmetische Mittel zugrunde, sind die Einkommen gesunken!

Anmerkung: Als Streumaß gehört die Standardabweichung σ zum arithmetischen Mittel, die mittlere lineare Abweichung zum Median, weil die Mittelwerte jeweils das Minimum der entsprechenden Streumaß-Funktionen darstellen. Eine Vermischung sollte nicht erfolgen.
Bei diesem Beispiel lässt sich noch diskutieren, welcher Mittelwert berechnet werden soll - der Median ist aber sicherlich zu bevorzugen.
Für andere Beispiele sind die genannten Mittelwerte aber nicht geeignet.
Generell sollte für jede vorliegende Werteliste über den geeigneten bzw. sinnvollen Mittelwert nachgedacht werden. Man denke nur an den Mittelwert verschiedener Füllhöhen von Gläsern mit gebogenem Rand (eben nicht zylinderförmig).

An dieser Stelle sollen noch zwei Beispiele folgen, die weitere bekannte Mittelwerte aufzeigen.

Beispiel 2:
Man erhält im ersten Jahr auf sein Kapital 5 % Zinsen, im zweiten Jahr 10 % Zinsen (die Reihenfolge ist egal). Welchen durchschnittlichen Zinssatz erhält man demzufolge pro Jahr?
Der durchschnittliche Zinssatz ist sicherlich derjenige, der - angewendet auf jedes Jahr - zu dem gleichen Endkapital führt.
Sei \(\overline{p}\) der durchschnittliche Zinssatz, K0 das Startkapital und K2 das Kapital nach zwei Jahren.
Dann gilt: K2 = K0 ⋅ 1,05 ⋅ 1,10 = K0 ⋅ (1 + \(\overline{p}\))2   →   (1 + \(\overline{p}\)) = 1,05⋅1,10 ≈ 1,0747   →   \(\overline{p}\) ≈ 7,47 %
Diesen Mittelwert nennt man das geometrische Mittel.

Beispiel 3:
Ein PKW fährt die 150 km lange Strecke von Husum nach Hamburg mit einer (konstanten) Geschwindigkeit von 100 km/h, auf dem Rückweg mit konstanten 75 km/h. Mit welcher Durchschnittsgeschwindigkeit ist er gefahren?
Die geeignete Durchschnittsgeschwindigkeit ist sicherlich diejenige, mit der auf der gesamten Strecke gefahren werden muss, um die 300 km in der gleichen Zeit zurückzulegen wie im Beispielfall.
Kleine Anleihe aus der Physik für gleichförmige Bewegungen: Weg = Geschwindigkeit ⋅ Zeit oder kürzer    s = v ⋅ t.
Die Strecke Husum-Hamburg sei s = 150 km, die Geschwindigkeit für den Hinweg sei v1 = 100 km/h und daraus die Zeit für den Hinweg t1 = 1,5 h. Entsprechend für den Rückweg (bei gleicher Weglänge s) v2 = 75 km/h sowie daraus t2 = 2 h.
Sei \(\overline{v}\) die Durchschnittsgeschwindigkeit auf der gesamten Strecke 2 ⋅ s   →   2 ⋅ s = \(\overline{v}\) ⋅ tG   →   \(\overline{v}\) = 2⋅stG    (*)
Die benötigte Gesamtzeit beträgt tG = t1 + t2 = sv1 + sv2 = 1,5 h + 2 h = 3,5 h.
Setzt man nun tG in die Formel (*) ein, erhält man: \(\overline{v}\) = 2⋅stG = 2⋅ssv1+sv2 = 21v1+1v2 = 21150+175 = 100 km/h


Nachfolgend eine kleine Zusammenfassung. Seien x1, x2, ... , xn die Urwerte.

Name Formel für n = 2 allgemein
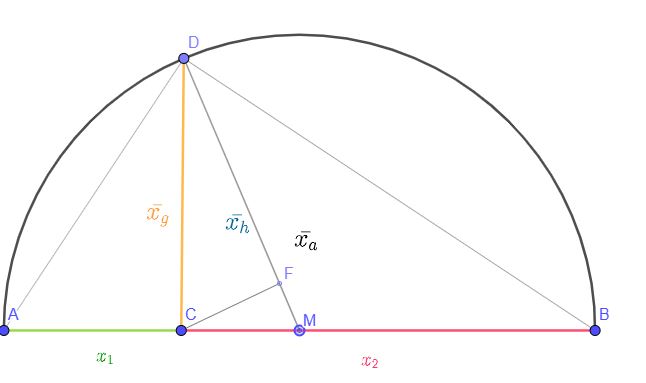
arithmetisches Mittel xa $$\overline{x}_a~=~\frac{x_1+x_2}{2}$$ \( \overline{x}_a~=~\frac{x_1+x_2+...+x_n}{n}\) \(~=~\frac{1}{n} \cdot \sum_{i=1}^{n} x_i\)
geometrisches Mittel xg $$\overline{x}_g~=~\sqrt{x_1 \cdot x_2}$$ \( \overline{x}_g~\) \(=~\large \sqrt[n]{x_1 \cdot x_2 \cdot ... \cdot x_n}\)
harmonisches Mittel xh $$\overline{x}_h~=~\frac{2}{\frac{1}{x_1}+\frac{1}{x_2}}$$ \( \overline{x}_h~=\) \(~\frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}}\)
Median m arithmetisches Mittel von x1 und x2 mittlerer Wert der geordneten Liste:
n gerade: x(n+1)/2
n ungerade: arithmetisches Mittel von xn/2 und xn/2 + 1



Arithmetisches, geometrischer und harmonisches Mittel lassen sich auch graphisch anschaulich darstellen.

Die Länge der Strecke AC sei der Wert x1, die Länge der Strecke CB der Wert x2.

Arithmetisches Mittel:
Um den Mittelpunkt M der Strecke AB wird ein Halbkreis gezeichnet. Der Radius dieses Halbkreises (AM = MB = MD) entspricht wegen der Konstruktion dem arithmetischen Mittel \(\overline{x}_a\) der Werte x1 und x2.

Geometrisches Mittel:
Das Dreieck ABD ist aufgrund des Satzes von Thales rechtwinklig. Nach dem Höhensatz des Euklid entspricht das Quadrat über der Höhe CD dem Produkt der beiden Hypothenusenabschnitte: h2 = CD2 = x1 ⋅ x2. Die Länge der Strecke CD stellt deshalb das geometrische Mittel \(\overline{x}_g\) der Werte x1 und x2 dar.

harmonisches Mittel:
Auch das Dreieck CMD ist rechtwinklig. Wendet man den Kathetensatz des Euklid auf dieses Dreieck an, ist das Quadrat über der Kathete CD gleich dem Produkt aus der Hypothenuse MD und dem zugehörigen Hypothenusenabschnitt FD:

\( CD^2~=~MD \cdot FD~~~\rightarrow~~~ FD ~= ~\frac{CD^2}{MD}~=~ \)\(\large \frac{x_1 \cdot x_2} {\frac{x_1+x_2}{2}}~= \) \(\large ~\frac{2}{\frac{1}{x_1}+\frac{1}{x_2}}\)\(~~(wegen~ \frac{1}{x_1}+\frac{1}{x_2}~=~\frac{x_1 + x_2}{x_1 \cdot x_2})\)

Die Länge der Strecke FD entspricht deshalb dem harmonischen Mittel \(\overline{x}_h\) der Werte x1 und x2.

Man erkennt: \(\overline{x}_h\) ≤ \(\overline{x}_g\) ≤ \(\overline{x}_a\)
Die Gleichheitszeichen gelten nur, falls x1 und x2 gleich sind.

Selbstredend bilden die angeführten Mittelwerte nur eine kleine Auswahl an möglichen Mittelwerten. Der 'richtige' oder 'vernünftige' Mittelwert hängt vom jeweiligen Kontext ab.