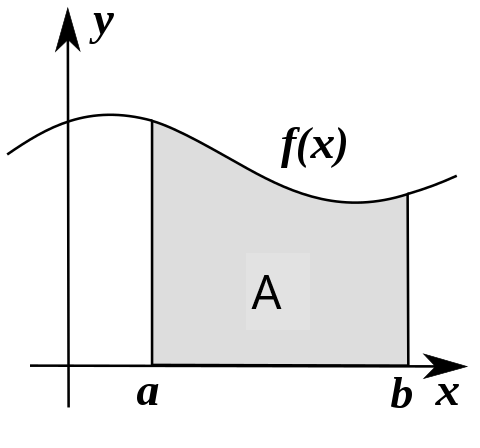
In der Schule wird der RiemannscheBernhard Riemann (1826-1866) Bedeutender Mathematiker, der in Göttingen lehrte. Integralbegriff verwendet, d.h. man verbindet mit dem Integral einer Funktion f über einem Intervall [a,b] - geschrieben - den Flächeninhalt A, den der Graph von f mit der x-Achse im Intervall [a,b] einschließt.
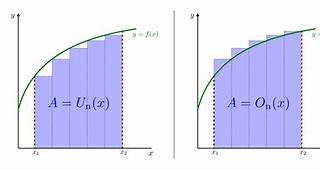
Um diesen Flächeninhalt einer krummlinig begrenzten Fläche zu ermitteln, beschreibt man in diese Fläche Rechtecke ein ( Stichwort: Untersumme U bzw Obersumme O) und lässt die Anzahl n dieser Rechtecke gegen unendlich gehen. Für n → ∞ ergeben Untersumme und Obersumme denselben Wert. Das Vorgehen führt auf den Begriff der Stammfunktion F ist eine Stammfunktion zur Funktion f, falls F'(x) = f(x) gilt. Ist F(x) eine Stammfunktion, so auch F(x) + c mit c ∈ ℝ, weil ein konstanter Summand bei der Ableitung herausfällt. F einer Funktion f und mündet in den Hauptsatz der Differential- und Integralrechnung:
.
Das gesuchte Integral wird berechnet, indem die Grenzen des Intervalls in die Stammfunktion f eingesetzt werden und die Differenz dieser Funktionswerte bestimmt wird!
Die Schwierigkeit besteht nun darin, eine Stammfunktion F zu der Funktion f zu finden. Und - schlimmer - in vielen Fällen existiert keine Stammfunktion in geschlossener Form! Man ist bei der Lösung von Integralen deshalb manchmal auf Näherungsverfahren angewiesen! Ein bekanntes Beispiel ist die in der Stochastik als Verteilungskurve auftretende GaußJohann Carl Friedrich Gauß (1777-1855) deutscher Mathematiker, der in Göttingen lehrte. Er galt schon wegen seiner überragenden Leistungen zu Lebzeiten als Princeps mathematicorum (Fürst der Mathematik).-Funktion f(x) = .
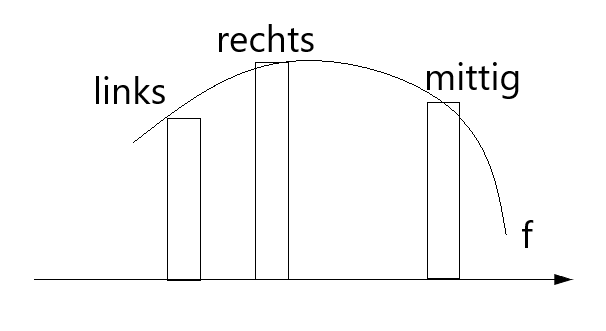
Dieses Verfahren beruht auf dem Einbeschreiben von Rechtecken gleicher Breite in die dem Integral zugeordnete Fläche. Dabei ist die Lage der den Rechtecken
zugeordneten Stützpunkte auf dem Funktionsgraphen im Prinzip beliebig: meist befinden sie sich links, rechts oder sind mittig angeordnet.
Außer der Funktion f und dem Intervall [a,b] ist nur die Anzahl n der Rechtecke anzugeben, die einbeschrieben werden. Je größer n desto genauer wird die Näherung.
Die Rechtecke besitzen alle die gleiche Breite .
Die Summe An der Flächeninhalte der Rechtecke beträgt
\( A_n = \) \( \Delta x \cdot f(a +\frac {1}{2} \Delta x) + \Delta x \cdot f(a + \frac {3} {2} \Delta x) \) \( + ... + \Delta x \cdot f(a + \frac {(2 n - 1)}{2} \cdot \Delta x) \) \(= \Delta x \cdot \sum_{i=1}^{n} f(a + \frac {(2 i - 1)}{2} \Delta x) \)
Im Bild sind vier Rechtecke mittig im Intervall [a,b] einbeschrieben.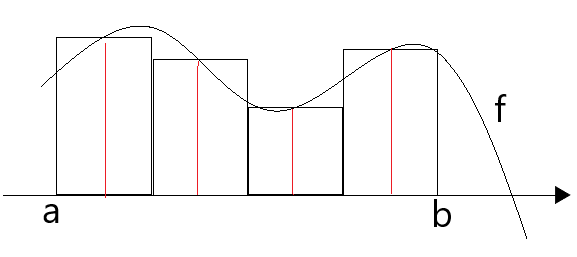
Anmerkung: In den unten anklickbaren Berechnungen werden für das Rechteckverfahren mittige Stützpunkte verwendet.
Es werden durch je zwei aufeinanderfolgende Stützstellen Sehnen gezeichnet. Die Flächeninhalte der dadurch einbeschriebenen Trapeze werden summiert.
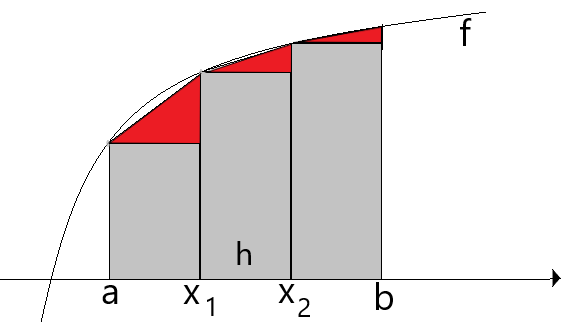Die Flächeninhalte der rot eingezeichneten Dreiecke werden zusätzlich zu den Flächeninhalten der grauen Rechtecke (s. Rechteckverfahren) berücksichtigt.
Es werden n Trapeze einbeschrieben. Alle Trapeze besitzen die gleiche 'Höhe' h =. Der Flächeninhalt des Trapezes zwischen den Stellen x1 und x2 beträgt dann beispielsweise
A = .
Addiert man alle Flächeninhalte der n Trapeze auf, werden folglich die Funktionswerte der 'inneren' Stützstellen doppelt gezählt, an den Stellen a und b nur einfach.
Man erhält demnach die Summe der n Trapezflächeninhalte:
$$ A_n = \frac {h}{2} (f(a) + f(b) + 2 \cdot \sum_{i=1}^{n-1} f(a + i \cdot h))$$Es werden durch je drei aufeinanderfolgende Stützstellen Parabelbögen gelegt und die Flächeninhalte unter den Parabelbögen summiert.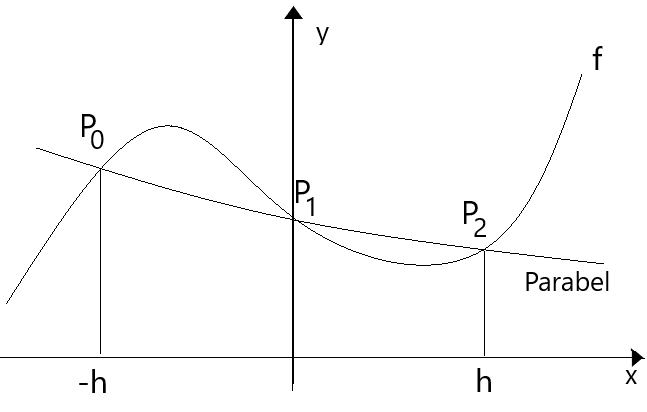
Eine Parabel ist durch drei Stützpunkte gegeben. Zuerst betrachten wir den Spezialfall eines Parabelbogens, dessen Abszissen der drei Stützpunkte symmetrisch zum Ursprung liegen. Die Parabel verläuft dann durch die Punkte P0( -h / f(-h) ) , P1( 0 / f(0) ) und P2( h / f(h) ).
Die Parabel sei gegeben durch f(x) = a·x2 + b·x + c.
Aus den Bedingungen
f(0) = c
f(-h) = a·h2 - b·h + c
f(h) = a·h2 + b·h + c
Daraus folgt: b = sowie a = .
Das Integral über der Parabel ergibt
$$\int_{-h}^{h} (a \cdot x^2 + b \cdot x + c)~ dx = \frac {2 \cdot a \cdot h^3} {3} + 2 \cdot c \cdot h$$Setzt man nun noch die Koeffizienten a und c ein, erhält man die KeplerscheJohannes Kepler (1571-1630), deutscher Astronom. Er stellte die Fassregel 1615 auf. Fassregel als Näherungsausdruck für das Integral über f im Intervall [-h , h]:
$$\int_{-h}^{h} f(x)~dx \sim \frac {h} {3} ~ (f(-h) + 4 \cdot f(0) + f(h))$$Fügt man nun n Segmente dieser Art (also der Breite 2h) nebeneinander, wobei die Parabeln nicht 'glatt' ineinander übergehen, werden die Randstützpunkte mit Ausnahme des ersten und des letzten jeweils doppelt, die mittleren Stützpunkte vierfach gezählt.
Die spezielle Wahl der Abszissen spielt keine Rolle, denn man kann die die Kurven in x-Richtung verschieben, ohne an dem eingeschlossenen Flächeninhalt etwas zu ändern.
So erhält man als numerische Integration nach Simpson:
Natürlich könnten auch Graphen ganzrationaler Funktionen höherer Ordnung als 2 zur näherungsweisen Berechnung herangezogen werden. Der Aufwand wäre aber beträchtlich.
Funktion f(x) =
linke Grenze a = rechte Grenze b =
| Rechteck / Sehnentrapez | Simpson | ||
|---|---|---|---|
| Anzahl Rechtecke (Trapeze): | Anzahl Parabelbögen: | ||