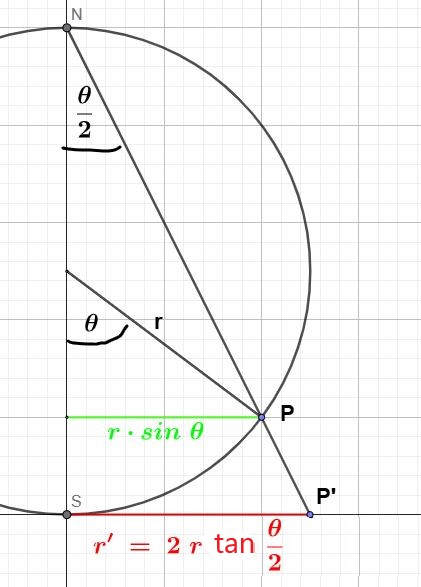
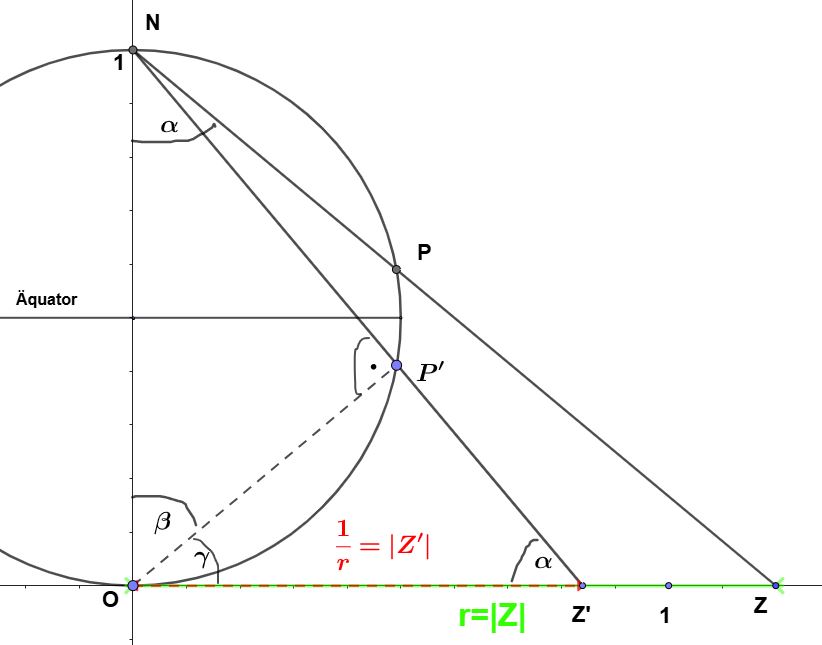
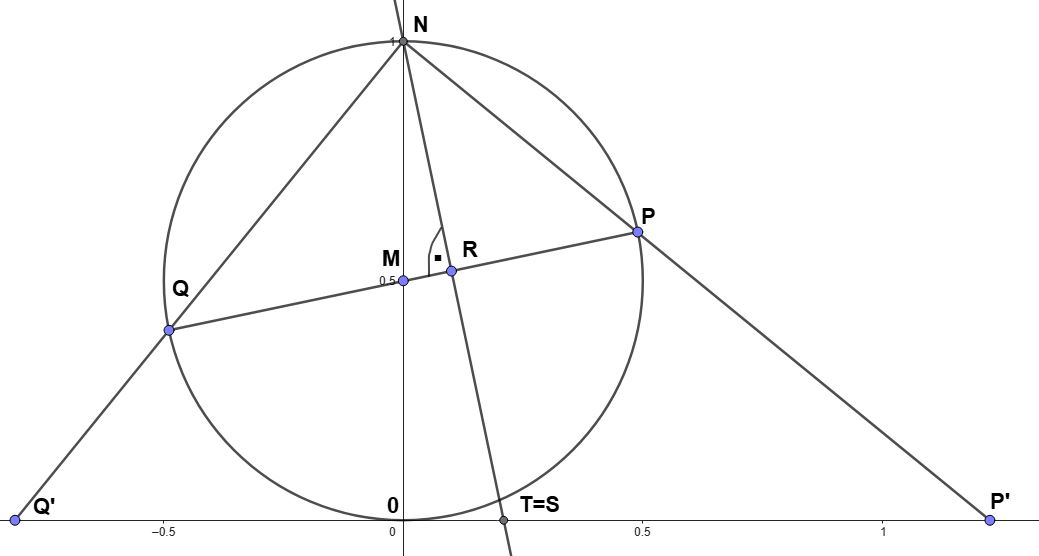
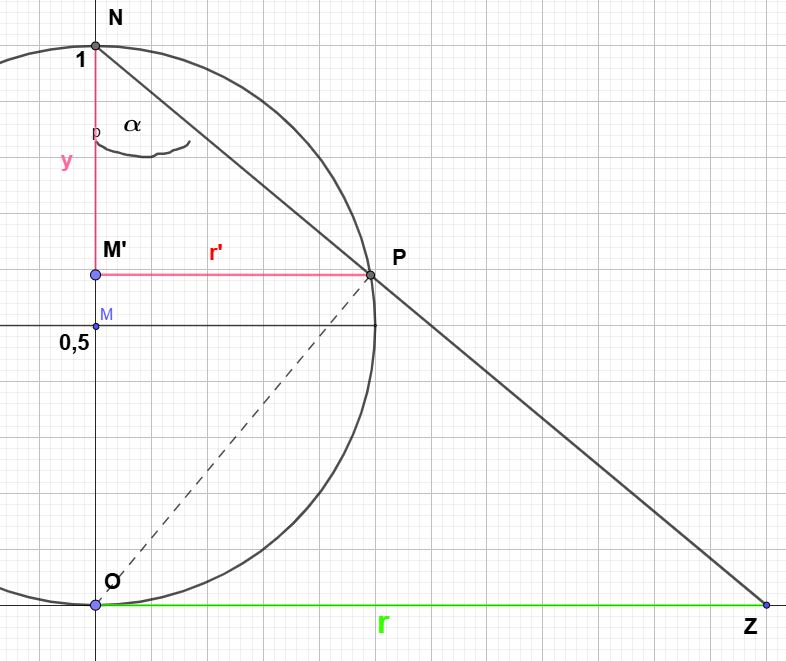
a) Mittelpunkt m = -1 und Radius r = \(\sqrt{3}\)
b)
i) Mittelpunkt m = i und Radius r = \(\sqrt{5}~~~\rightarrow~~~\)\(zz^{*}+iz-iz^{*}-4=0\)
ii) Mittelpunkt m = 1 und Radius r = \(\sqrt{mm^{*}-\gamma}=\sqrt{1-(-24)}=5~~~\rightarrow~~~\)|z - 1| = 5
iii) Mittelpunkt m = -i und Radius r = \(\sqrt{mm^{*}-\gamma}=\sqrt{1-0}=1~~~\rightarrow~~~\)|z + i| = 1
zu 2.
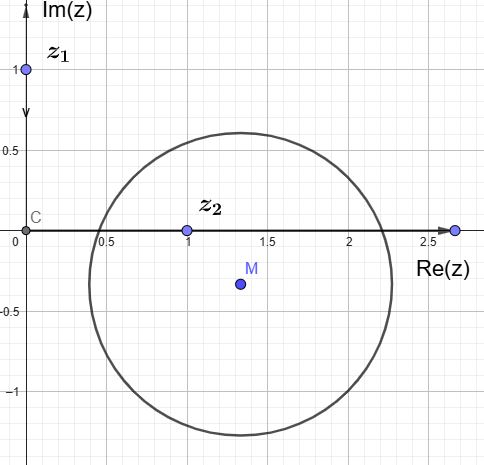 Alle Punkte z, die von den Punkten \(z_1\) und \(z_2\) das feste Abstandsverhältnis a : b besitzen,
Alle Punkte z, die von den Punkten \(z_1\) und \(z_2\) das feste Abstandsverhältnis a : b besitzen, genügen der Gleichung \(\large \frac{|z-z_1|}{|z-z_2|}~=~\frac{a}{b}\).
Eingesetzt ergibt:
\(\large \frac{|z-i|}{|z-1|}\) = 2.
Quadriert und umgeformt:
\(zz^{*}+iz-iz^{*}+1~=~4\cdot (zz^{*}-z-z^{*}+1)\)\(~~~\rightarrow~~~zz^{*}-\frac{1}{3}(4+i)z-\frac{1}{3}(4-i)z^{*}+1~=~0\)
Das ist eine Kreisgleichung mit dem Mittelpunkt m = \(\frac{1}{3}\)(4 - i) und dem Radius \(r=\sqrt{mm^{*}-\gamma}=\sqrt{\frac{17}{9}-1}=\frac{2}{3}\sqrt{2}\)
Der Kreis heißt Kreis des Apollonius.
zu 3.
i) Aus b = i = α + βi und γ = 1 folgt:
\(m=-\large \frac{\alpha}{\beta}~=~-\frac{0}{1}\)\(~=~0\)
\(b=-\large \frac{\gamma}{2\beta}~=~-\frac{1}{2\cdot 1}\)\(~=~-\frac{1}{2}\)
Dies ist eine Gerade parallel zur reellen Achse im Abstand 0,5 unterhalb der reellen Achse.
ii)
Aus b = 1 - i = α + βi und γ = 2 folgt:
\(m=-\large \frac{\alpha}{\beta}~=~-\frac{1}{-1}\)\(~=~1\)
\(b=-\large \frac{\gamma}{2\beta}~=~-\frac{2}{2\cdot (-1)}\)\(~=~2\)
zu 4.
Die Gerade geht durch den Punkt a = 1 + 0i und der Richtungsvektor beträgt v = 1 + 2i.
Die Steigung erhält man aus dem Richtungsvektor m = \(\frac{2}{1}\) = 2.
Um den imaginären Achsenabschnitt zu ermitteln, muss der Realteil von f(t) = 0 gelten.
f(t)) = 1 + 0i + (1+2i)⋅t → Re(f(t)) = 1 + 1⋅t = 0 → t = -1.
Eingesetzt f(-1) = 1 + 0i + (1+2i)⋅(-1) = 0 - 2i → Achsenabschnitt b = -2.
Um zu entscheiden, ob der Punkt \(z_0\) ein Element der Geraden ist, setzt man \(z_0\) in die Geradengleichung ein. Existiert ein t, ist der Punkt ein Element der Geraden, sonst nicht.
0,5 + 1,5i = 1 + 0i + (1+2i)⋅t.
Man erhält 2 reelle Gleichungen (Real- und Imaginärteil):
0,5 = 1 + 1⋅t → t = -0,5
1,5 = 0 + 2⋅t → t = -0,75
Kein gemeinsames t → \(z_0\) ist kein Element der Geraden.
Man kann es in diesem Fall auch ohne Rechnung entscheiden. Da a = 1 + 0i ein Punkt der Geraden ist, kann nicht auch \(z_0\) = 1 + 1,5i ein Punkt der Geraden sein. Denn dann wäre es eine Gerade parallel zur imaginären Achse. Das ist für Parameterformen nicht erlaubt.
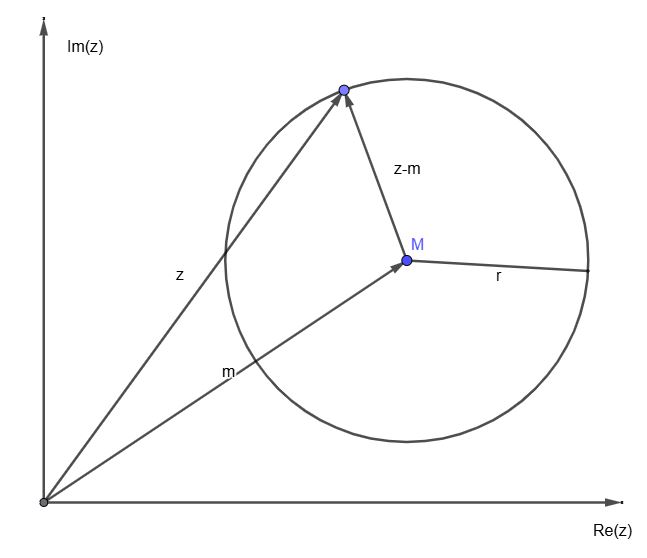
 Durch die Verwendung von Ungleichungen können flächenhafte Punktmengen dargestellt werden.
Durch die Verwendung von Ungleichungen können flächenhafte Punktmengen dargestellt werden.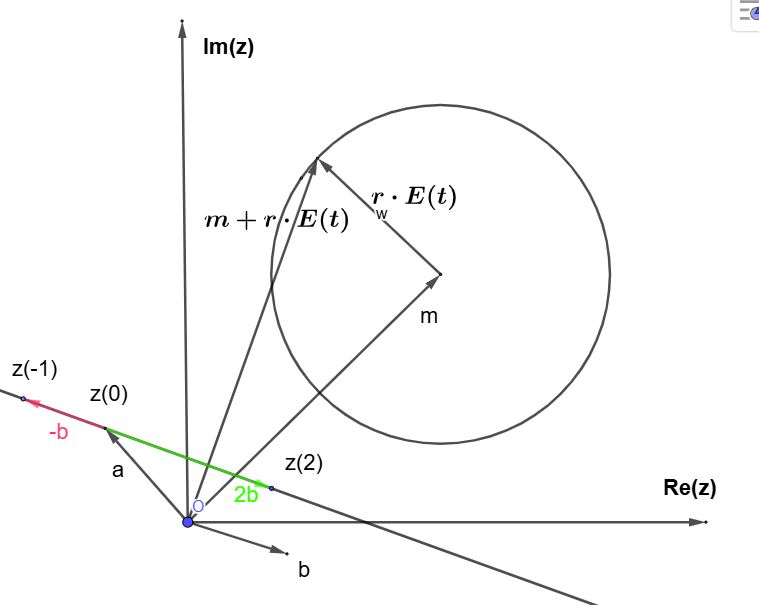 Kreislinie mit Mittelpunkt m∈ \(\mathbb{C}\) und Radius r∈\(\mathbb{R}^+\) in Parameterform: {z(t)| z(t) = m + r⋅E(t) und 0≤t≤2π}.
Kreislinie mit Mittelpunkt m∈ \(\mathbb{C}\) und Radius r∈\(\mathbb{R}^+\) in Parameterform: {z(t)| z(t) = m + r⋅E(t) und 0≤t≤2π}.
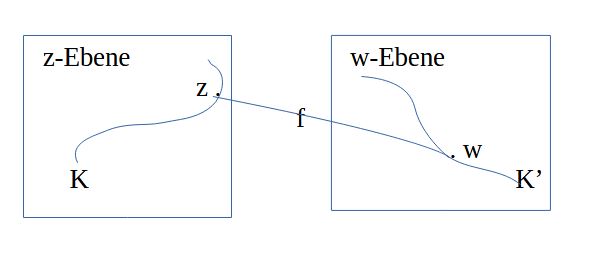 In der Mathematik werden für reelle Funktionen Graphen (oder Kurven) in einem Koordinatensystem gezeichnet: ein Element auf der x-Achse wird genau ein Element auf der y-Achse zugeordnet.
In der Mathematik werden für reelle Funktionen Graphen (oder Kurven) in einem Koordinatensystem gezeichnet: ein Element auf der x-Achse wird genau ein Element auf der y-Achse zugeordnet.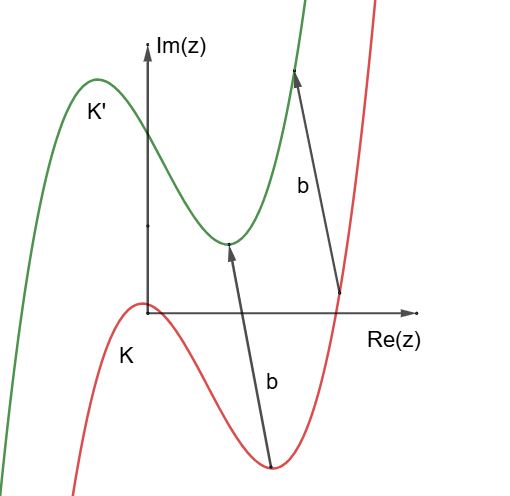 Fasst man die komplexen Zahlen als Vektoren in der Zahlenebene auf, erhält man den Bildvektor w
durch Addition des Urbildvektors z mit einem konstanten Vektor b.
Fasst man die komplexen Zahlen als Vektoren in der Zahlenebene auf, erhält man den Bildvektor w
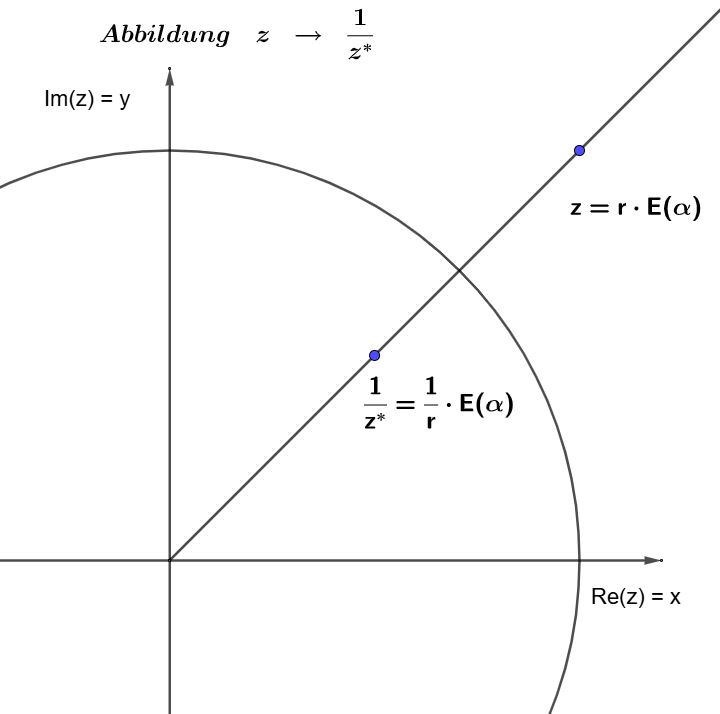
durch Addition des Urbildvektors z mit einem konstanten Vektor b.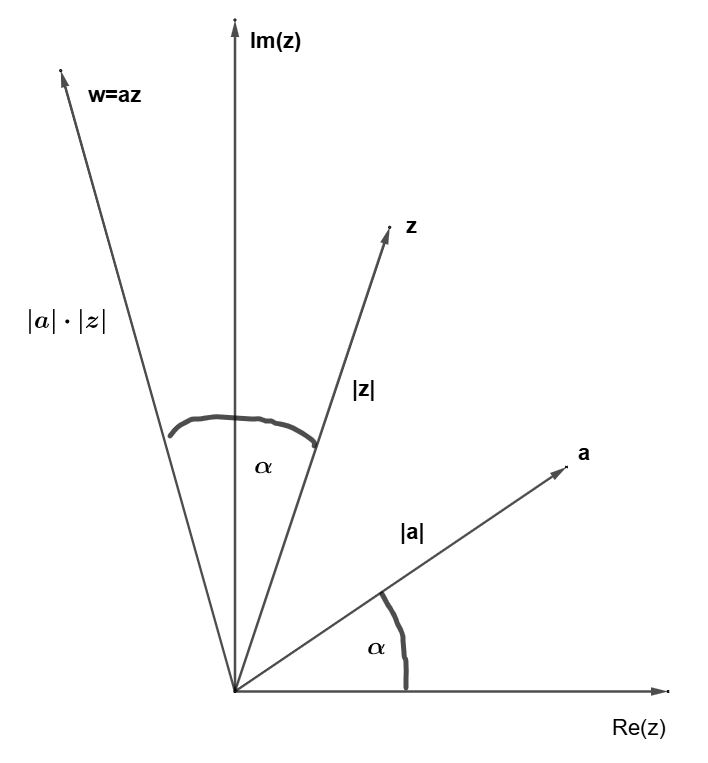 Um die geometrische Bedeutung dieser Abbildung zu erfassen, werden sowohl z als auch a ≠ 0 in Polarform dargestellt:
Um die geometrische Bedeutung dieser Abbildung zu erfassen, werden sowohl z als auch a ≠ 0 in Polarform dargestellt: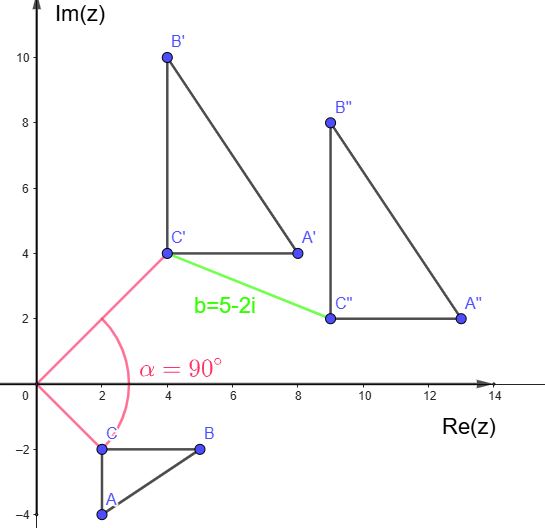 Verknüpft man die Funktionen
Verknüpft man die Funktionen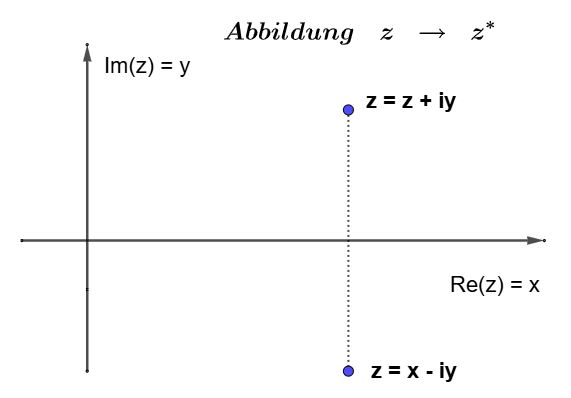
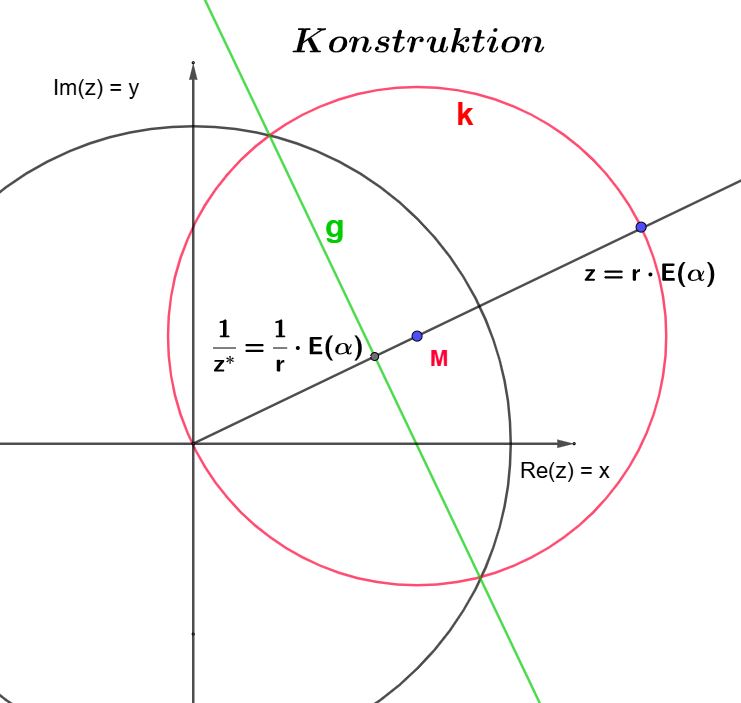
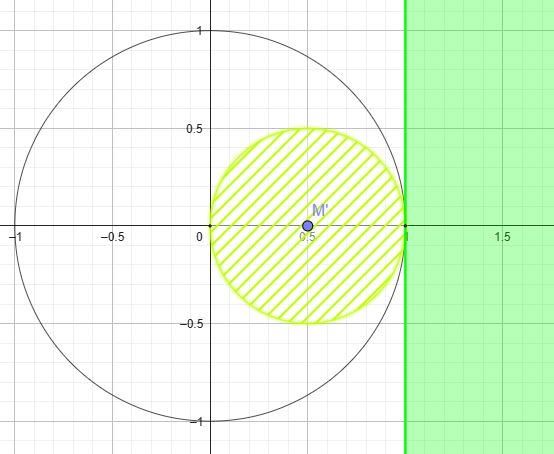
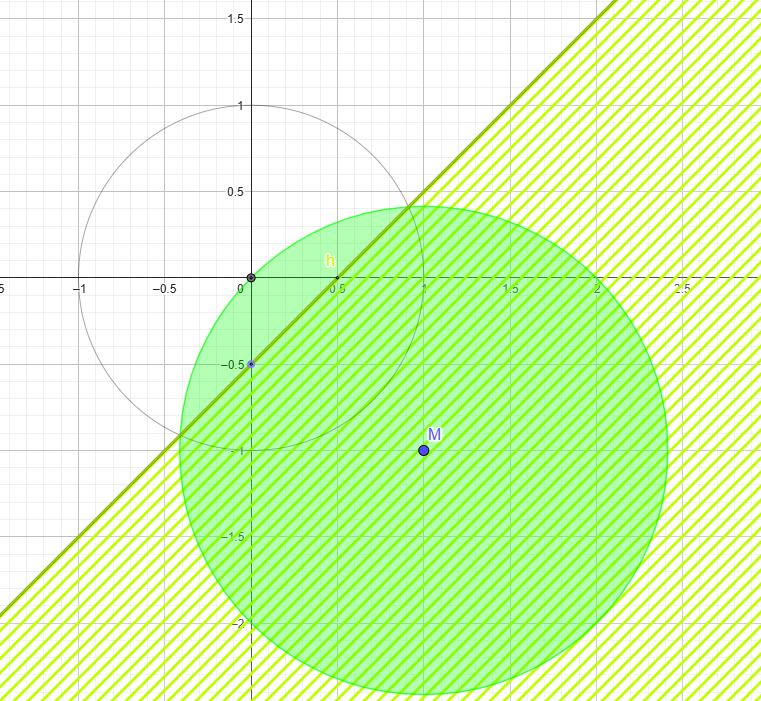 a) Zuerst wird der Bildkreis ermittelt. Anschließend bildet man einen (beliebigen) Punkt des Ur-Gebietes ab. Das Bild des Kreises bildet dann aufgrund der Gebietstreue der Abbildung die Begrenzung des Bildgebietes.
a) Zuerst wird der Bildkreis ermittelt. Anschließend bildet man einen (beliebigen) Punkt des Ur-Gebietes ab. Das Bild des Kreises bildet dann aufgrund der Gebietstreue der Abbildung die Begrenzung des Bildgebietes.