René Descartes (1596-1650) war ein französischer Philosoph, Mathematiker und Naturwissenschaftler.
René Descartes (1596-1650) war ein französischer Philosoph, Mathematiker und Naturwissenschaftler.
Geschichtliches
 René Descartes (1596-1650) war ein französischer Philosoph, Mathematiker und Naturwissenschaftler.
René Descartes (1596-1650) war ein französischer Philosoph, Mathematiker und Naturwissenschaftler.
 Leonhard Euler (1707-1783) war ein schweizer Mathematiker und Naturwissenschaftler.
Leonhard Euler (1707-1783) war ein schweizer Mathematiker und Naturwissenschaftler.
 Abraham de Moivre(1667-1754) war ein französischer Mathematiker.
Abraham de Moivre(1667-1754) war ein französischer Mathematiker. Carl Friedrich Gauss (1777-1855) war ein deutscher Mathematiker, Geodät und Naturwissenschaftler.
Carl Friedrich Gauss (1777-1855) war ein deutscher Mathematiker, Geodät und Naturwissenschaftler.
Inhalt
2. Erste Beispiele inkl. Division komplexer Zahlen
3. Polarform und Gaußsche Zahlenebene
3.1. Polarform komplexer Zahlen
4.1. Kreisteilungsgleichung zn = 1
5. Fundamentalsatz der Algebra
1. Einführung und Definition
[an+1,bn+1] ⊆ [an,bn]
mit bn - an → 0
Beispiel: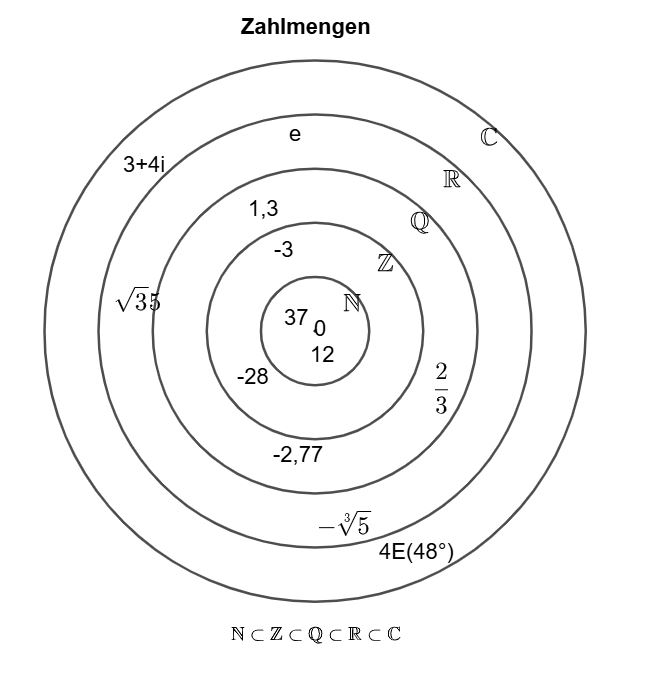 Die Menge \(\mathbb{R}\) umfasst damit rationale und irrationale Zahlen.
Die Menge \(\mathbb{R}\) umfasst damit rationale und irrationale Zahlen.i2 = -1
Definition: komplexe Zahlen
Die Menge \(\mathbb{C}\) der komplexen Zahlen wird dargestellt durch
\(\boldsymbol{\mathbb{C}~=~\{a+bi~|~a,b\in\mathbb{R}\}}~~~mit~i^2=-1\)
Zu beachten: \(i^2=-1~~,~~i^3=i^2\cdot i=-i~~,~~i^4=i^2\cdot i^2=1\).
Höhere Potenzen als 1 von i können entsprechend umgewandelt werden.
2. Erste Beispiele inkl. Division komplexer Zahlen
2.1. Beispiele
2.2. Aufgaben
3. Polarform und Gaußsche Zahlenebene
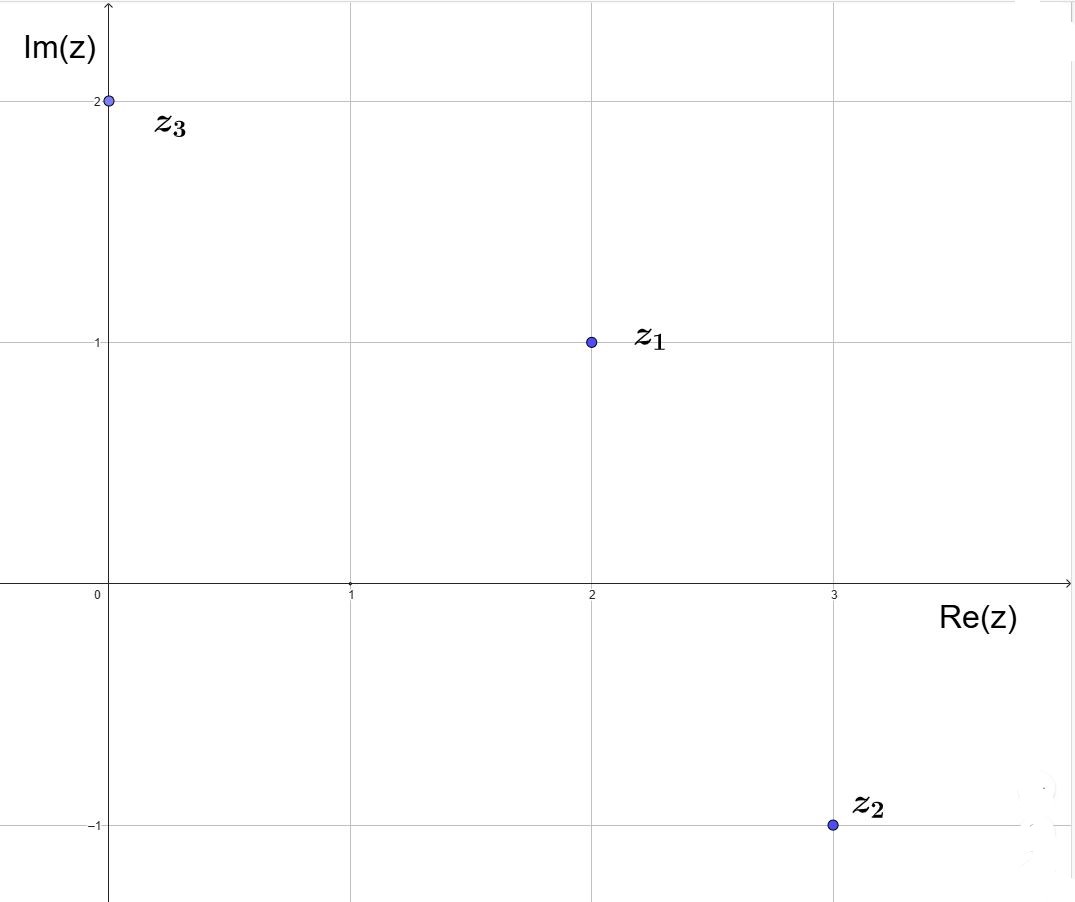
3.1. Polarform komplexer Zahlen
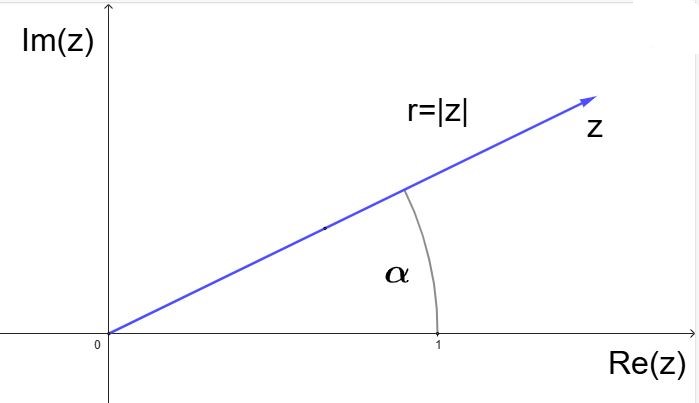
(a , b) ↔ (r , α)
a = r cos α
b = r sin α
r = \(\sqrt{a^2+b^2}\)
α = arctan \(\large \frac{b}{a}\) 2. und 3. Quadrant: +180° , 4. Quadrant: +360°
Sonderfälle Re(z)-Achse: b = 0 , a > 0 → α = 0° ; b = 0 , a < 0 → α = 180°
Im(z)-Achse: a = 0 , b > 0 → α = 90° ; a = 0 , b < 0 → α = 270°
r = |z| = \(\sqrt{a^2+b^2}=\sqrt{z\cdot z^*}\).
z = a + bi = r⋅E(α) mit E(α) = cos α + i sin α
E(α) = cos α + i sin α = \(e^{i\alpha}~~~~~\) (Eulersche Formel)
Der Zusammenhang erschließt sich über die Taylorreihen-Entwicklung der involvierten Funktionen.1. E(α) = E(α + 2⋅n⋅π) ∀ α ∈ \(\mathbb{R}\) , n ∈ \(\mathbb{Z}\)
insbesondere E(0) = 1
2. |E(α)| = 1
3. \(E(\alpha_1)\cdot E(\alpha_2)~=~E(\alpha_1+\alpha_2)\)
insbesondere für \(\alpha_1=-\alpha_2=\alpha~gilt:~E(\alpha)\cdot E(-\alpha)~=~E(0) = 1\)
\(d.h.~E(-\alpha)~ist~zu~ E(\alpha)~reziprok:~\frac{1}{E(\alpha)}=E(-\alpha)\)
außerdem gilt: \((E(\alpha))^2~=~ E(2\alpha)~bzw.~(E(\alpha))^n~=~ E(n\alpha)\) , n ∈ \(\mathbb{N}\)
cos (α + β) = cos α ⋅ cos β - sin α ⋅ sin β
sin (α + β) = cos α ⋅ sin β + sin α ⋅ cos β
Die Sonderfälle ergeben sich durch Einsetzen in die Eigenschaft 3- Letzteren mit vollständiger Induktion.3.2. Aufgaben
4. Wurzeln komplexer Zahlen
4.1. Kreisteilungsgleichung zn = 1
\(\large \alpha_i~=~\frac{0°+i \cdot 360°}{n}~=~\frac{0°}{n}~+~\frac{i}{n} \cdot 360°\)\(~~~~mit~~i\in~\{0,...,n-1\}\)
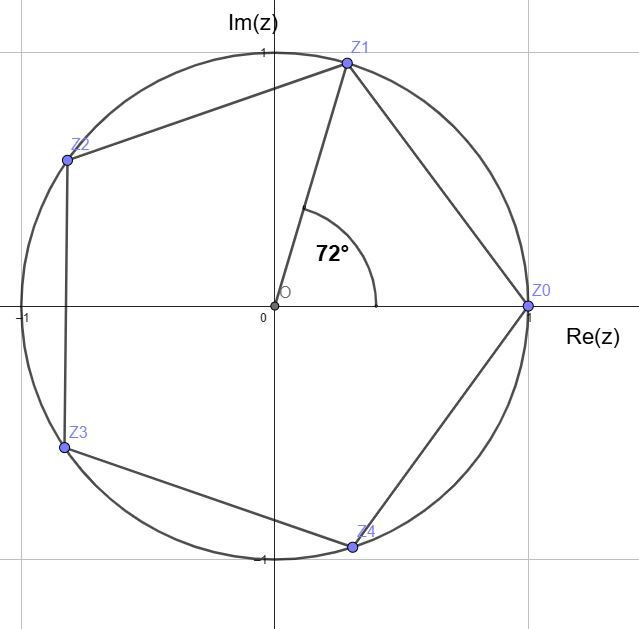
4.2. Gleichung zn = r E(α)
\(\large z_i~=~\sqrt[n]{|r|} \cdot E(\frac{\alpha}{n}~+~\frac{i}{n} \cdot 360°)\)\( ~~~~mit~~i\in~\{0,...,n-1\}\)
4.3. Aufgaben
5. Fundamentalsatz der Algebra
Fundamentalsatz der Algebra
Jede Gleichung n. Grades (n ≥ 1) der Form
\(a_nz^n~+~a_{n-1}z^{n-1}~+~...~+~a_1z~+~a_0~=~0\)
mit \(a_i~\in ~\mathbb{C}~~,~~i~\in~\{0,...,n\}\) hat in \(\mathbb{C}\) mindestens eine Lösung.
6. Anwendungen
1.1. Bewegungen
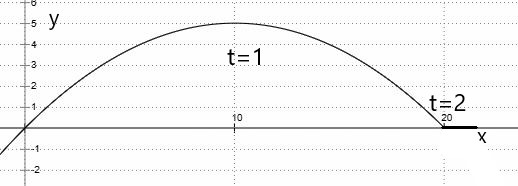
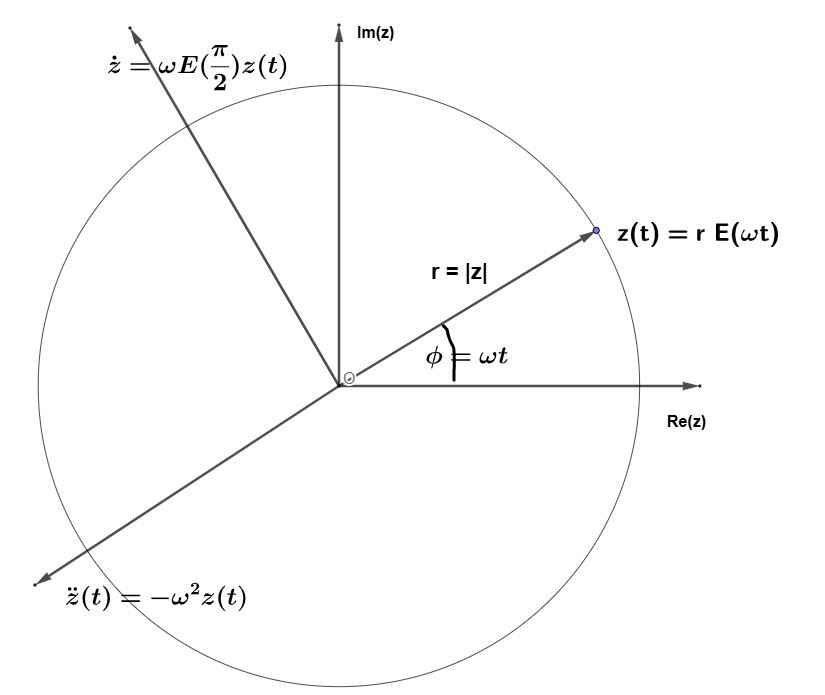
| Ort | \(z(t) = r ~E(\omega t)\) | |
| Geschwindigkeit | \(\dot{z}(t)=\omega~ E(\frac{\pi}{2})\cdot z(t)\) | mit \(|\dot{z}| = \omega~ |z| =\omega~ r\) |
| Beschleunigung | \(\ddot{z}(t)= -\omega^2~z(t)\) | mit \(|\ddot{z}| = \omega^2~ |z| =\omega^2~ r\) |
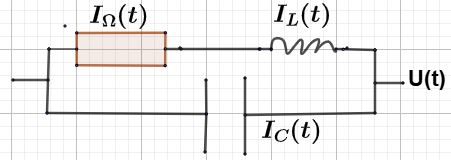
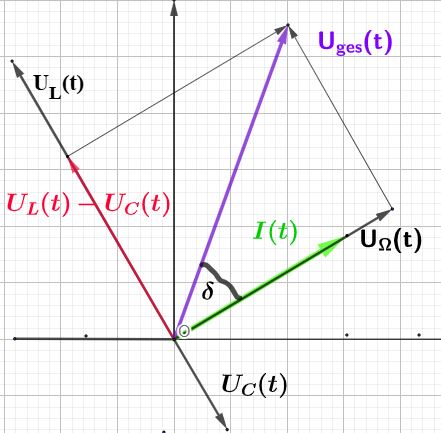
6.2. Wechselstrom
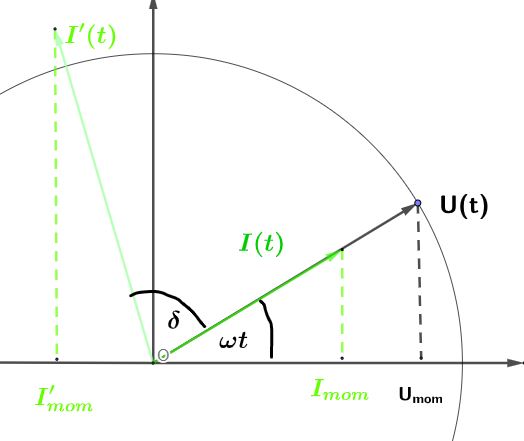
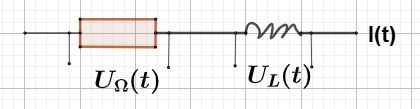
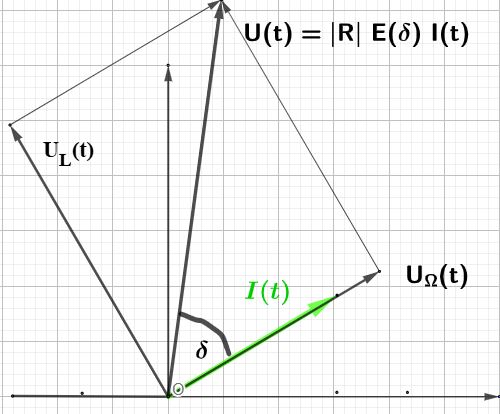
\( \large R~=~R_1~+~R_2 \)
\( \Large \frac{1}{R}~=~\frac{1}{R_1}~+~\frac{1}{R_2} \)
6.3. Pythagoräische Zahlen
\(a^2~+~b^2~=~c^2\)
\(a^2~+~b^2~=~c^2~~~\leftrightarrow~~~\large \frac{a^2}{c^2}~+~\frac{b^2}{c^2}\)\(~=~1~~~\leftrightarrow~~~\large \frac{a}{c}+\frac{b}{c}\)\(i~\in~\mathbb{S}\)
Die pythagoräischen Zahlentripel (bis auf Vielfache) entsprechen den
rationalen Punkten auf dem Viertelkreis \(\mathbb{V}\) des Einheitskreises im I. Quadranten.
1. Es gilt: \(\large \frac{|z+i|}{|z-i|}\)\(~=~1~~~\leftrightarrow~~~\)z ist reell\(~~~~~\)
2. Die Abbildung f: \(\mathbb{R}~~\rightarrow~~\mathbb{S}/\{1\}\)
\(~~~f(x)~=~z~=~\large \frac{x+i}{x-i}\)\(~=~\large \frac{(x+i)(x+i)}{(x-i)(x+i)}\)\(~=~\large \frac{x^2-1}{x^2+1}\)\(+\large \frac{2x}{x^2+1}\)i
\(~~~\)bildet die reelle Achse auf den Einheitskreis ab.
\(~~~\)Rationale Zahlen in \(\mathbb{R}\) werden auf rationale Punkte in \(\mathbb{S}/\{1\}\) abgebildet (rationale Terme).
\(~~~\)Für rationale Bildpunkte auf dem Viertelkreis \(\mathbb{V}\) gilt:
\(~~~\)Urbild x > 1 (beachte den Realteil von f(x)).\(~~~~\)
3. Die Umkehrabbildung \(f^{-1}\): \(\mathbb{S}/\{1\}~~\rightarrow~~\mathbb{R}\)
\(~~~f^{-1}(z)~=~\large \frac{-iz-i}{-z+1}\) existiert.\(~~~~\)
| a | b | \(\mathbf{a^2-b^2}\) | 2 ab | \(\mathbf{a^2+b^2}\) |
| 2 | 1 | 3 | 4 | 5 |
| 3 | 1 | 8 | 6 | 10 |
| 3 | 2 | 5 | 12 | 13 |
| 4 | 1 | 15 | 8 | 17 |
6.4. Aufgaben